掌握度分秒、角度制与弧度制之间的快速换算秘籍

度分秒、角度制、弧度制快速换算方法详解

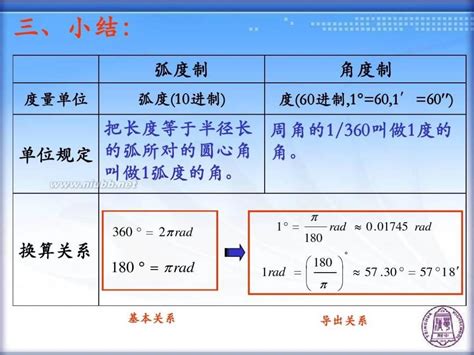
在数学、物理和工程等领域，角度的度量是非常重要的。我们通常使用的角度度量方式有度分秒制、角度制和弧度制。这三种度量方式各有优劣，了解并快速转换它们对许多人来说都非常有价值。

一、度分秒制

度分秒制是古代天文学家使用的一种表示角度的方法，也常见于地理坐标系统中。它通过将1度分成60分，每分再分成60秒来精细地表示角度。

换算关系：

1度 = 60分

1分 = 60秒

例子：

将48°30'45"转换为度：

先将秒转换为分：45" ÷ 60 = 0.75'

加上原来的分：30' + 0.75' = 30.75'

再将分转换为度：30.75' ÷ 60 = 0.5125°

加上原来的度：48° + 0.5125° = 48.5125°

二、角度制

角度制，也称十进制角度，是用一个数从0到360（或者-180到180）来表示一个角。这是最常见也是最容易理解的角度表示方法。

例子：

45°就表示为45度，没有任何进一步的换算。

三、弧度制

弧度制则是基于半径来度量角度的方法。一个圆的周长与半径的比值，即2π，是360度，因此1弧度被定义为角度所对应的弧长与半径相等的那部分弧。

换算关系：

1弧度 ≈ 57.295779513°

1° = π/180 弧度

弧度制的一些特点：

π弧度表示半圆，2π弧度表示整个圆。

弧度制在进行三角函数的计算时非常方便，尤其是当使用微积分和泰勒级数展开时。

四、快速换算方法

1. 度分秒制与角度制的换算

将度分秒转换为角度制时，我们可以先将秒转换为分，再将分转换为度，然后求和。反之，我们可以使用四舍五入和适当的数学运算将角度制转换为度分秒。

将度分秒转换为角度制：

如之前48°30'45"的例子，首先进行秒到分的转换，再进行分到度的转换，最后求和。

将角度制转换为度分秒：

以54.324°为例：

分 = (54.324° - 取整(54.324°)) × 60 = 19.44'

去掉上一步中小数点后剩余的0.44'

秒 = (0.44' - 取整(0.44')) × 60 = 26.4" ≈ 26"（四舍五入）

结果为54°19'26"

2. 角度制与弧度制的换算

由于π弧度等于180度，我们可以使用这一换算关系来进行快速转换。

将角度制转换为弧度制：

只需将角度乘以π/180。例如，90°转换为弧度为90 × π/180 = π/2 弧度。

将弧度制转换为角度制：

只需将弧度乘以180/π。例如，π/4弧度转换为角度为π/4 × 180/π = 45°。

3. 度分秒与弧度制的换算

因为度分秒制和弧度制之间没有直接的换算关系，我们通常需要将度分秒转换为角度制，再将角度制转换为弧度制。

将度分秒转换为弧度制：

先按照前述方法将度分秒转换为角度制，然后使用角度制到弧度制的换算公式进行转换。

将弧度制转换为度分秒：

先将弧度制转换为角度制，然后将角度制按照前述方法转换为度分秒。

五、简化计算的工具与技巧

尽管我们提供了一些基础的换算方法，但在实际操作中，许多人更倾向于使用计算器或计算机程序来简化这些计算。以下是几种简化计算的工具和技巧：

使用计算器：

现代计算器通常内置有角度和弧度之间的转换功能，甚至可以直接处理度分秒的计算。

编写或利用现成的转换程序：

使用编程语言（如Python、C等）编写一个简单的转换程序，或使用已经开发好的库和函数，可以极大地方便我们的计算。

记住常见值的换算：

记住一些常见角度（如30°、45°、60°等）的弧度表示，以及常见弧度（如π/6、π/4、π/3等）的角度表示，可以节省很多时间。

估算与近似：

在进行不需要极高精度的计算时，可以适当地使用估算和近似，以减少计算步骤和提高计算速度。

六、结语

掌握度分秒、角度制和弧度制之间的快速换算方法对于处理与角度相关的数学和物理问题至关重要。无论是在日常生活、科学研究还是工程设计中，了解并能准确转换这些角度单位都是一项重要的技能。希望本文的介绍能帮助读者更好地理解和应用这些换算方法，提升解决相关问题的能力。