揭秘圆周率：探寻隐藏的数学奥秘与规律

圆周率，这个自古以来便令无数数学家与学者着迷的无理数，不仅承载着几何学的奥秘，更是连接数学、物理乃至宇宙规律的神秘桥梁。它不仅是圆的周长与直径之比，更是一个在数字世界中永不重复的无穷序列，蕴藏着自然界的深刻规律与宇宙的无限可能。

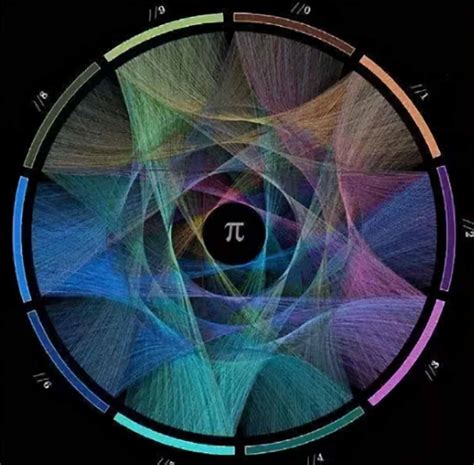
几何之美：圆周率的直观展现

谈及圆周率π，最直观的联想便是圆形——这一自然界中最完美的几何形态之一。在古希腊哲学家毕达哥拉斯学派眼中，圆是宇宙的完美象征，而π则是这一完美的量化表达。从圆规画圆到测量其周长与直径，π的存在让几何学家能够精确计算圆的面积、周长以及相关的几何量，构建起几何学大厦的基石。随着数学的发展，π的精确值成为衡量一个国家数学水平的重要标志，从阿基米德的多边形逼近法到祖冲之的“密率”，再到现代的电子计算机计算，人类对π的探索史，就是一部生动的数学进步史。

数字之谜：π的无理性与超越性

π的迷人之处，不仅在于其几何意义，更在于其作为一个无理数的独特性质。无理数，即无法表示为两个整数之比的数，π的无限不循环小数特性，让无数试图找到其精确表达式的数学家望洋兴叹。18世纪末，数学家勒让德证明了π是无理数，这一发现颠覆了人们对于数的传统认知，开启了无理数研究的新篇章。随后，19世纪末，德国数学家林德曼证明了π的超越性，即π不满足任何非零的整系数多项式方程，这一发现进一步巩固了π在数学中的特殊地位，也预示着π与代数数之间的深刻界限。

数学与物理的桥梁：π在宇宙中的应用

圆周率π不仅仅是一个数学常数，它在物理学乃至宇宙学中也有着意想不到的应用。爱因斯坦的广义相对论中，π与宇宙曲率、时空结构紧密相连。在宇宙微波背景辐射的研究中，科学家们通过分析辐射的微小涨落，试图揭示宇宙早期的结构形成，而π在这一过程中扮演了关键角色，它影响着辐射波动的周期性和分布模式。此外，在量子力学中，π出现在波函数的周期性条件、能级计算公式等多个方面，展现出数学与物理的和谐统一。

随机性与混沌：π中的正态分布与随机游走

深入探究π的数字序列，会发现其隐藏着惊人的统计规律。巴塞尔问题揭示了π与自然对数底e之间的神秘联系，而π的数字序列中，数字的分布呈现出惊人的正态分布特征，这在一定程度上揭示了随机现象背后的数学秩序。更令人惊奇的是，π的数字序列还被用来模拟随机游走问题，即在二维平面上，一个点随机上下左右移动，其路径长度与π的某个特定形式密切相关。这种联系不仅加深了我们对随机过程的理解，也展示了π作为连接确定性与随机性的桥梁作用。

信息论与编码：π的压缩与无限信息

在信息论领域，圆周率π同样展现出非凡的魅力。根据香农的信息论，任何信息都可以用比特（bit）来量化，而π作为一个无限不循环小数，理论上包含了无限的信息量。这意味着，如果我们能将π的所有数字都记录下来，理论上就可以存储任何形式的信息。尽管这在现实中不可能实现，但这一概念启发了数学家和计算机科学家们探索更有效的数据压缩方法和信息编码技术。事实上，一些研究者已经利用π的数字序列来加密信息，虽然这种方法的安全性仍有待商榷，但它无疑展示了π在信息时代的潜在应用。

哲学与艺术：π的无限与人类认知的边界

从哲学的角度来看，π的无限性挑战了人类对确定性和无限性的理解。它让我们意识到，即便是在看似简单的几何形状中，也隐藏着宇宙的无限奥秘。这种无限性不仅体现在π的数值上，更体现在人类对知识的追求和探索上。正如大卫·鲍伊在歌曲《无限》中唱道：“圆周率，它永无止境，就像我们的生活。”π的无限性激发了人类对未知的好奇心和探索欲，推动了科学的进步和文明的发展。

在艺术领域，π也成为了创作灵感的源泉。艺术家们以π的数字序列为基础，创作出了一系列令人惊叹的作品，从音乐到绘画，从雕塑到数字艺术，π的每一个数字都被赋予了新的生命和意义。这些作品不仅展现了π的美学价值，也反映了人类对数字世界的独特理解和创造力。

结语

综上所述，圆周率π不仅是一个数学常数，它更是连接数学、物理、信息论、哲学乃至艺术的桥梁。它的无限不循环小数特性，挑战了人类的认知极限，激发了人类对知识的渴望和探索精神。从古希腊哲学家对圆的哲学思考，到现代科学家对π的深入研究，π的历史就是一部人类智慧的探索史。在这个过程中，我们不仅加深了对自然界规律的理解，也拓宽了人类认知的边界，推动了科学的进步和文明的繁荣。圆周率π，这个看似简单的数学符号，实则蕴含着宇宙的无限奥秘和人类的无限可能。