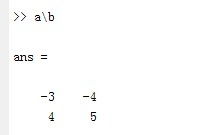复数的概念与运算是什么？

带你走进复数的奇妙世界

在数学的浩瀚宇宙中，有一个令人着迷的领域，它超越了实数轴的束缚，将我们带入了一个更为广阔、深邃的维度——复数。这个听起来略带神秘色彩的数学概念，其实就在我们身边，与我们日常的计算、物理现象乃至自然界的奥秘紧密相连。今天，就让我们一起揭开复数的神秘面纱，探索它背后的概念与运算之美。

想象一下，你正在解决一个方程，比如x²=-1。在实数世界里，这似乎是个无解之题，因为任何正实数的平方都是正的，而任何负实数的平方则是正的（但值更大）。但数学家们从不满足于现状，他们渴望探索未知，于是，一个大胆的想法诞生了：创造一个数，让它的平方等于-1。这个数，就是复数中的“虚数单位”i，它满足i²=-1。

复数，简单来说，就是实数和虚数单位的和，形式为a+bi，其中a和b是实数，i是虚数单位。这个看似简单的定义，却打开了一个全新的数学世界的大门。复数不仅仅是数学家的玩具，它们在物理学、工程学、电子学等领域都有着广泛的应用。比如，交流电的电压和电流可以用复数来表示，这使得电路的分析和计算变得更加简洁明了。

现在，让我们来深入了解一下复数的运算。就像实数可以进行加减乘除一样，复数也有自己的一套运算规则。

加法与减法

对于两个复数a+bi和c+di，它们的加法运算非常直观：只需将实部与实部相加，虚部与虚部相加即可。所以，(a+bi)+(c+di)=(a+c)+(b+d)i。减法运算也是类似的，只需将第二个复数的每个部分都取反（即改变符号），然后进行加法运算。因此，(a+bi)-(c+di)=(a-c)+(b-d)i。

乘法

复数的乘法运算稍微复杂一些，但同样遵循分配律和结合律等基本法则。两个复数相乘时，需要按照分配律展开，即(a+bi)×(c+di)=ac+adi+bci+bdi²。由于i²=-1，所以bdi²可以化简为-bd。因此，(a+bi)×(c+di)=(ac-bd)+(ad+bc)i。这个运算过程虽然看似繁琐，但当我们熟练掌握后，就能迅速得出结果。

除法

复数的除法运算可能是最具有挑战性的部分。为了消除分母中的虚数部分，我们需要与其共轭复数相乘。共轭复数是改变虚数部分的符号得到的复数，对于复数a+bi，其共轭复数为a-bi。当我们用分子和分母都乘以分母的共轭复数时，分母就会变成一个实数（因为(a+bi)×(a-bi)=a²-b²是一个实数），从而可以方便地进行除法运算。

举个例子，如果我们想计算(2+3i)/(4+5i)，我们可以先将分子和分母都乘以分母的共轭复数4-5i，得到：

(2+3i)(4-5i)/((4+5i)(4-5i))=(8-10i+12i-15i²)/(16-25i²)

由于i²=-1，所以上式可以化简为：

(8+2i+15)/(16+25)=(23+2i)/41

最后，我们可以将这个分数拆分成实部和虚部：

(23/41)+(2/41)i

通过这个过程，我们可以看出，虽然复数的除法运算比加法和乘法复杂一些，但只要我们掌握了共轭复数的概念，就能轻松应对。

除了基本的四则运算外，复数还可以进行开方、对数、指数等运算。这些运算在复数平面上（一个由实部和虚部构成的二维平面）上有着直观的几何意义。比如，复数的开方运算可以看作是复数平面上点到原点的距离的开方，同时考虑该点与正实轴之间的夹角的一半。

复数还有一个重要的性质——共轭对称性。对于任意复数a+bi，其共轭复数为a-bi。这两个复数在复数平面上关于实轴对称。这个性质在复数的运算和解析几何中都有着重要的应用。

复数不仅在数学领域内大放异彩，还在物理学、工程学等领域中发挥着不可替代的作用。在物理学中，复数可以用来描述波动现象（如光波、声波等）的振幅、相位和频率等特性。在工程学中，复数被广泛应用于信号处理、控制系统、电路设计等领域。此外，复数还与量子力学、相对论等现代物理理论紧密相连，为科学家们提供了强有力的数学工具。

随着科技的发展，复数在现实生活中的应用也越来越广泛。比如，在图像处理领域，复数可以用来进行边缘检测、图像滤波等处理；在通信系统中，复数被用来描述信号的调制和解调过程；在金融领域，复数则被用来进行风险评估、期权定价等复杂计算。

复数的概念虽然源于对无解方程的求解，但它却发展成了一个独立而完整的数学体系。在这个过程中，数学家们不断挖掘复数的性质和应用，推动了数学和相关领域的发展。如今，复数已经成为现代数学和物理学不可或缺的一部分，为我们探索未知世界提供了强大的武器。

当然，复数的奇妙之处还远远不止于此。随着我们对复数更深入的研究和理解，相信它会为我们揭示更多自然界的奥秘和数学的魅力。所以，如果你对复数还感到陌生或困惑的话，不妨从现在开始，踏上这段探索复数世界的奇妙旅程吧！你会发现，这个看似神秘的概念其实充满了乐趣和惊喜。