如何在Excel中计算标准差?
Excel标准差:数据波动性的精准度量
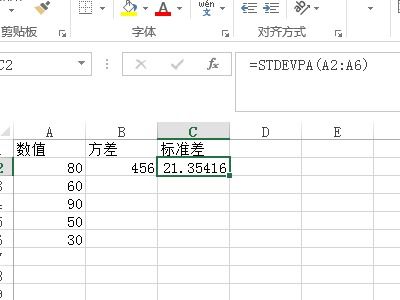
在数据分析的广阔领域中,Excel作为一款功能强大的电子表格软件,凭借其丰富的函数库和便捷的操作方式,成为了众多数据分析师和普通用户处理数据的首选工具。其中,标准差函数(STDEV.P和STDEV.S)作为衡量数据波动性的重要指标,在数据分析过程中扮演着举足轻重的角色。本文将从标准差的概念、Excel中标准差函数的应用、标准差的解读以及标准差在数据分析中的实际应用等多个维度,深入探讨Excel标准差的相关知识。

一、标准差的概念
标准差(Standard Deviation)是统计学中用于描述数据集波动性或离散程度的一个关键指标。它表示的是数据集中的各个数值与均值(平均值)之间的偏差程度。标准差越大,说明数据集中的数值与均值之间的偏差越大,即数据的波动性越大;反之,标准差越小,说明数据集中的数值与均值之间的偏差越小,即数据的波动性越小。
标准差的计算公式为:

标准差 = √((每个数值-均值)² 的平均值)
这个公式直观地反映了标准差是如何通过计算每个数值与均值的偏差,并取这些偏差的平方的平均值的平方根来得到的。
二、Excel中标准差函数的应用
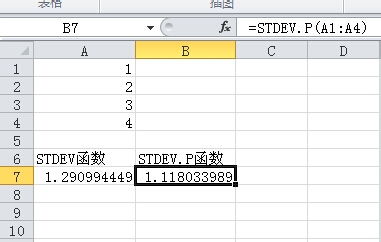
在Excel中,计算标准差主要通过两个函数来实现:STDEV.P和STDEV.S。这两个函数虽然都用于计算标准差,但在处理包含重复数据的数据集时有所不同。
1. STDEV.P函数
STDEV.P函数用于计算基于整个数据样本(即总体)的标准差。当数据集中的每一个数据点都被视为总体的一部分时,应使用STDEV.P函数。其计算公式为:
STDEV.P = √((Σ(x-μ)²)/N)
其中,Σ表示求和,x表示数据集中的每一个数值,μ表示均值,N表示数据点的总数。
在Excel中,使用STDEV.P函数的语法为:STDEV.P(number1,[number2],...),其中number1、number2等表示要计算标准差的数值或数值区域。
2. STDEV.S函数
STDEV.S函数则用于计算基于样本数据的标准差。当数据集中的数据点是从总体中随机抽取的样本时,应使用STDEV.S函数。其计算公式与STDEV.P类似,但在分母上有所不同,因为它考虑了样本大小与总体大小之间的差异,从而进行了适当的调整。
在Excel中,使用STDEV.S函数的语法与STDEV.P类似,但需要注意的是,STDEV.S函数在计算过程中会考虑样本的偏差,因此结果可能会与STDEV.P有所不同。
三、标准差的解读
标准差作为衡量数据波动性的重要指标,其数值本身并不直接反映数据的具体分布情况,但可以通过与其他统计量(如均值、中位数等)的结合使用,为我们提供关于数据集分布特征的深入洞察。
1. 数据波动性的度量
标准差越大,说明数据集中的数值与均值之间的偏差越大,即数据的波动性越大。这种波动性可能源于多种因素,如市场需求的波动、生产过程中的误差等。通过计算标准差,我们可以对数据的波动性进行量化分析,从而更准确地把握数据的分布特征。
2. 数据异常值的检测
在数据分析过程中,异常值(即与大多数数据点显著不同的数值)可能会对分析结果产生重要影响。通过计算标准差,我们可以设置一个合理的范围(如均值±3倍标准差),用于检测数据集中的异常值。如果某个数值超出了这个范围,那么它很可能是一个异常值。
3. 数据正态性的判断
正态分布是统计学中一种重要的分布类型,它具有许多优良的性质和广泛的应用。通过计算标准差和均值,我们可以绘制出数据的直方图或概率密度函数图,从而直观地判断数据是否服从正态分布。如果数据的分布呈现出钟形曲线且标准差适中,那么可以初步认为数据服从正态分布。
四、标准差在数据分析中的实际应用
标准差在数据分析领域具有广泛的应用价值,它可以帮助我们更好地理解和分析数据集的分布特征、波动性以及异常值等问题。以下是一些具体的应用场景:
1. 市场研究
在市场研究中,标准差可以用于衡量消费者需求的波动性。例如,通过分析不同时间段内消费者对某种产品的需求量数据,我们可以计算出需求量的标准差,从而了解消费者需求的波动情况。这对于制定生产计划、库存管理以及市场营销策略等方面都具有重要的指导意义。
2. 质量控制
在质量控制领域,标准差可以用于衡量生产过程中的波动性。通过计算生产线上不同批次产品的质量标准差,我们可以评估生产过程的稳定性和一致性。如果标准差较大,说明生产过程中的波动性较大,可能存在质量问题或生产过程中的不稳定因素。这有助于及时发现并解决问题,提高产品质量和生产效率。
3. 金融风险管理
在金融领域,标准差被广泛应用于风险管理中。例如,通过计算股票收益率的标准差,我们可以评估股票价格的波动性。波动性越大,说明股票价格的变动越剧烈,投资者面临的风险也越大。这有助于投资者制定合理的投资策略和风险管理措施。
4. 社会科学研究
在社会科学研究领域,标准差也被用于衡量不同群体之间的差异程度。例如,通过分析不同年龄段、性别或职业群体的收入水平数据,我们可以计算出收入水平的标准差,从而了解不同群体之间的收入差异情况。这对于制定相关政策、促进社会公平和经济发展等方面都具有重要的参考价值。
综上所述,Excel标准差作为衡量数据波动性的重要指标,在数据分析过程中具有广泛的应用价值。通过掌握标准差的概念、计算方法以及解读方法,我们可以更好地理解和分析数据集的特征和规律,从而为决策提供支持。
- 上一篇: 制作福州特色海鲜锅边的步骤
- 下一篇: 手机QQ账号被冻怎么办?快速解冻指南!
-
 Excel中标准差计算的实用教程资讯攻略11-23
Excel中标准差计算的实用教程资讯攻略11-23 -
 如何在Excel中轻松计算标准差?资讯攻略11-22
如何在Excel中轻松计算标准差?资讯攻略11-22 -
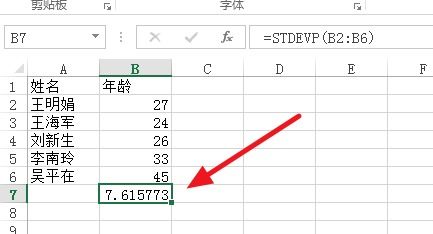 Excel中如何轻松计算标准差资讯攻略11-23
Excel中如何轻松计算标准差资讯攻略11-23 -
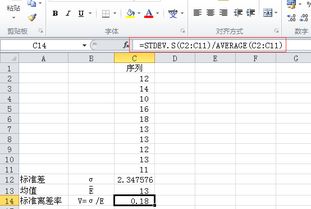 如何在Excel中使用标准差公式函数?资讯攻略12-03
如何在Excel中使用标准差公式函数?资讯攻略12-03 -
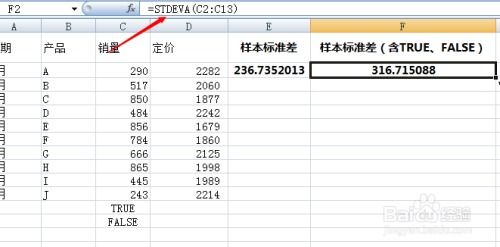 掌握Excel标准差计算:STDEV与STDEVA等函数的深度解析资讯攻略11-18
掌握Excel标准差计算:STDEV与STDEVA等函数的深度解析资讯攻略11-18 -
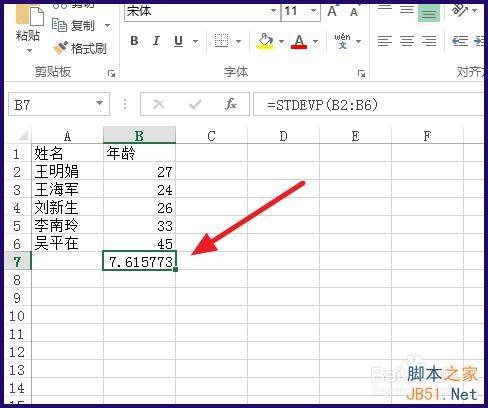 Excel中计算标准差的方法资讯攻略12-03
Excel中计算标准差的方法资讯攻略12-03












