轻松学会:如何保留两位有效数字
保留两位有效数字的方法

在科学计算、工程设计、财务分析等多个领域中,我们经常需要按照特定的格式或精度来表示数字。保留有效数字是一种重要的数值表示方法,它不仅可以减少数据的冗余,还能保证数值的精度和可读性。本文将详细介绍如何保留两位有效数字,帮助大家掌握这一实用的数值处理技术。

一、有效数字的概念

有效数字是指从左边第一个不是零的数字起,到精确到的位数止,所有的数字都叫做这个数的有效数字。例如,对于数字“123.456”,其有效数字是六位,分别是“1、2、3、4、5、6”。在保留有效数字时,需要注意以下几点:

1. 非零数字前的零不是有效数字。例如,“0.0056”的有效数字是“5、6”。
2. 有效数字的保留与小数点的位置无关,只与数字的位数和精度有关。
3. 整数部分只有一位数的数,如“8”,其有效数字是“8”。
二、保留两位有效数字的规则
保留两位有效数字,即要求将数值表示成只有两位有效数字的形式,同时尽量保持数值的精度和可读性。以下是保留两位有效数字的具体规则:
1. 确定数值的有效数字位数。
如果数值本身已经是两位或更少的有效数字,则无需进一步处理。
如果数值有多于两位的有效数字,则需要根据保留规则进行舍入。
2. 舍入规则
四舍五入法:这是最常用的舍入方法。观察第三位有效数字,如果它小于5,则第二位有效数字不变;如果它大于或等于5,则第二位有效数字加1。例如,“123.456”保留两位有效数字后变为“1.2×10^2”,“12.345”保留两位有效数字后变为“12”。
五舍六入五成双法:也被称为银行家舍入法。这种方法在四舍五入的基础上,对于第三位有效数字是5且其前后有效数字不同的情况,采取使结果末位数成为偶数的原则进行舍入。例如,“2.355”保留两位有效数字后变为“2.4”,“2.255”则保留为“2.2”。
3. 科学计数法表示
对于非常大的数或非常小的数,使用科学计数法可以更直观地表示其数量级。保留两位有效数字后,数值应表示为“a×10^n”的形式,其中a是1到10之间的数(包括1但不包括10),n是整数。
例如,“123456”保留两位有效数字后变为“1.2×10^5”,“0.000123456”保留两位有效数字后变为“1.2×10^-4”。
三、保留两位有效数字的具体步骤
以下是一个详细的示例,演示了如何将一个数值保留两位有效数字:
1. 数值分析:
给定数值:“12345.6789”。
观察数值的有效数字位数,这里是九位有效数字。
2. 确定保留形式:
由于数值较大,使用科学计数法表示会更合适。
3. 应用舍入规则:
将数值转换为科学计数法形式:“1.23456789×10^4”。
观察第三位有效数字(小数点后第三位),这里是“4”。
由于“4”小于5,根据四舍五入法,第二位有效数字“3”保持不变。
4. 最终表示:
数值保留两位有效数字后表示为:“1.2×10^4”。
四、常见数值的保留两位有效数字示例
1. 整数:
“12345”保留两位有效数字后变为“1.2×10^4”。
“8”保留两位有效数字后仍为“8”(因为已经是两位有效数字)。
2. 小数:
“0.00123456”保留两位有效数字后变为“1.2×10^-3”。
“123.456789”保留两位有效数字后变为“1.2×10^2”(科学计数法)或“120”(直接舍入到最接近的整数,但注意这不是科学计数法表示)。
3. 带有正负号的数值:
“-12345.6789”保留两位有效数字后变为“-1.2×10^4”。
“+0.0000876543”保留两位有效数字后变为“8.8×10^-5”(注意这里使用了五舍六入五成双法,因为第三位有效数字是5且其前一位是偶数8)。
五、保留两位有效数字的应用
保留两位有效数字在多个领域都有广泛应用:
1. 科学研究:在实验结果中保留有效数字可以确保数据的准确性和可读性。
2. 工程设计:在设计过程中,对参数进行保留有效数字的处理可以减少计算误差。
3. 财务分析:在财务报表中,保留有效数字可以确保数字的准确性和合规性。
4. 教育领域:在教学活动中,教授保留有效数字的方法可以帮助学生培养严谨的数值处理习惯。
六、注意事项
1. 理解精度:保留有效数字时,要注意理解并区分绝对精度和相对精度。绝对精度是指数值的绝对误差范围,而相对精度是指数值的相对误差范围。
2. 使用合适的工具:在计算器和编程语言中,通常有内置的函数或方法来处理有效数字的保留。使用这些工具可以简化处理过程并提高准确性。
3. 避免误解:在传递数值信息时,要确保接收者理解保留有效数字的意义和限制。避免由于误解而导致数据处理的错误。
通过本文的介绍,相信读者已经掌握了保留两位有效数字的方法。在实际应用中,应根据具体需求和场景选择合适的保留方式和舍入规则。同时,保持对数值精度的敏感性和准确性是确保数据处理质量的关键。
- 上一篇: 陈奕迅电影精选
- 下一篇: 如何设置五星红旗为头像
-
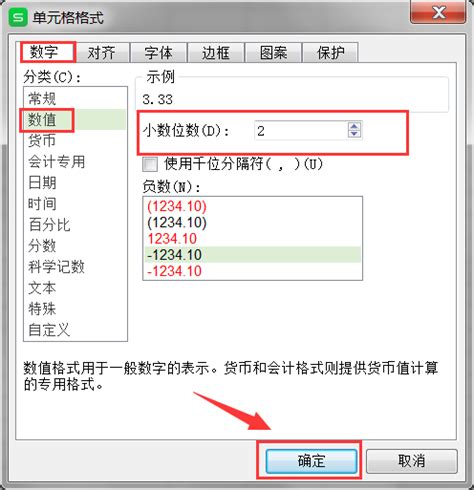 轻松学会保留数字到两位小数的方法资讯攻略11-16
轻松学会保留数字到两位小数的方法资讯攻略11-16 -
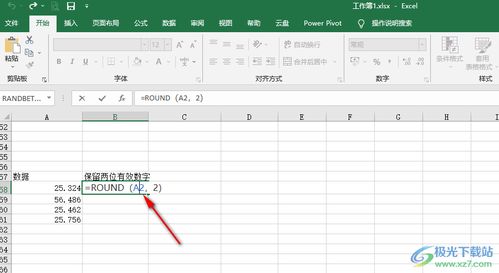 在Excel中保留数值至两位有效数字的方法资讯攻略12-01
在Excel中保留数值至两位有效数字的方法资讯攻略12-01 -
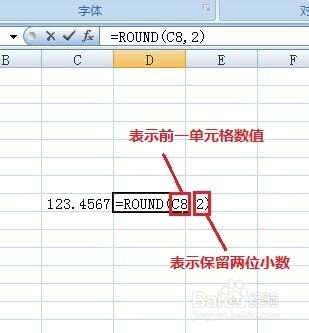 精准解读:保留两位有效数字的真正含义资讯攻略12-03
精准解读:保留两位有效数字的真正含义资讯攻略12-03 -
 如何在Excel表格中设置数字保留两位小数?资讯攻略11-15
如何在Excel表格中设置数字保留两位小数?资讯攻略11-15 -
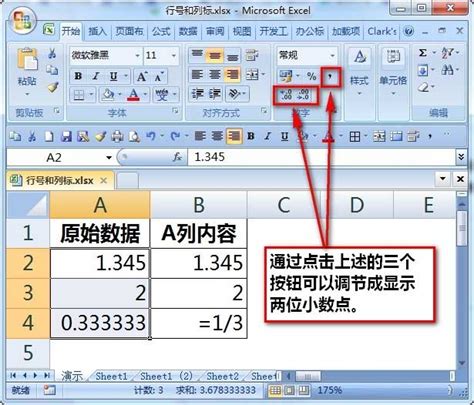 Excel轻松设置保留两位小数的方法资讯攻略11-19
Excel轻松设置保留两位小数的方法资讯攻略11-19 -
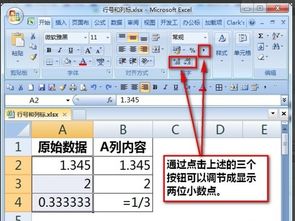 Excel技巧:轻松保留数值的两位小数资讯攻略12-02
Excel技巧:轻松保留数值的两位小数资讯攻略12-02












