RSD%的计算方法是什么？

RSD%的计算公式是怎么算的

在数据分析、科学研究以及模型预测等多个领域中，相对标准偏差（RSD%，Relative Standard Deviation）是一个至关重要的指标。它能够帮助我们评估数据的离散程度、预测模型的稳定性以及不同数列的变异程度。本文将详细介绍RSD%的计算公式及其相关应用，通过多个维度深入探讨其重要性。

一、RSD%的基本概念

RSD%，全称为相对标准偏差，也被称为变异系数、标准偏差系数或变动系数。它通过标准偏差与平均值的比值，乘以100%得出。具体公式为：

\[ RSD\% = \left( \frac{标准偏差}{平均值} \right) \times 100\% \]

这里的“标准偏差”是指数据集中各数据点与平均值之间的离散程度，用以衡量数据值偏离算术平均值的程度。而“平均值”则代表了数据的一般水平。通过RSD%，我们可以直观地了解数据点的变异程度或模型的预测精度。

二、标准偏差的计算

要计算RSD%，首先需要求出数据的标准偏差。标准偏差的计算过程如下：

1. 计算平均值：将所有数据点的总和除以数据点的数量，得到平均值（μ）。

2. 计算每个数据点与平均值的差值：对于数据集中的每个数据点（x），减去平均值（μ），得到差值（x - μ）。

3. 求差值的平方：将这些差值平方，以消除负值的影响。

4. 求和并计算方差：将所有平方值求和，然后除以数据点的数量减去1（n-1），得到样本方差。

5. 计算标准偏差：对样本方差开平方根，得到标准偏差（σ）。

用数学公式表示，标准偏差的计算过程如下：

\[ 标准偏差(σ) = \sqrt{\frac{\sum_{i=1}^{n} (x_i - μ)^2}{n - 1}} \]

其中，x_i 是数据集中的每个数据点，μ 是数据集的平均值，n 是数据点的数量。

三、RSD%的计算

一旦标准偏差和平均值被计算出来，就可以使用RSD%的公式得出结果。以下是计算RSD%的详细步骤：

1. 计算标准偏差：如上所述，使用数据点计算出标准偏差（σ）。

2. 计算平均值：使用所有数据点的总和除以数据点的数量，得出平均值（X）。

3. 计算RSD%：将标准偏差除以平均值，然后乘以100%，得到RSD%。

数学公式为：

\[ RSD\% = \left( \frac{σ}{X} \right) \times 100\% \]

四、RSD%的应用

RSD%作为衡量数据离散程度和模型预测能力的关键指标，广泛应用于各个领域。

1. 数据质量评估：在统计分析中，RSD%可用于评估数据的稳定性和一致性。较低的RSD%表明数据点之间的差异较小，数据质量较高。

2. 模型预测能力评估：在模型预测中，RSD%是衡量模型预测结果稳定性和精度的重要指标。通过比较不同模型的RSD%，可以快速判断哪个模型的预测结果更稳定、更接近实际情况。例如，在预测未来天气时，模型的RSD%越低，说明其预测结果越稳定，与实际观测值的偏差越小。

3. 变异程度比较：RSD%还可用于比较不同数列的变异程度。当不同总体的社会现象由于变异度指标的计量单位不同，或同类现象在平均数不等的情况下，不能直接用标准差进行对比时，可以通过计算RSD%来进行比较。这有助于了解不同数据集之间的相对差异程度。

五、实际案例

假设我们用一个模型预测了未来10天的温度，并记录了预测温度和真实温度。以下是具体数据：

| 日期 | 预测温度 | 真实温度 |

||||

| 1 | 25°C | 23°C |

| 2 | 27°C | 26°C |

| 3 | 28°C | 28°C |

| 4 | 30°C | 29°C |

| 5 | 32°C | 31°C |

| 6 | 33°C | 33°C |

| 7 | 35°C | 34°C |

| 8 | 37°C | 36°C |

| 9 | 38°C | 37°C |

| 10 | 40°C | 39°C |

通过计算，我们可以得到预测温度的标准差为4.47，平均值为32°C。因此，RSD%为：

\[ RSD\% = \left( \frac{4.47}{32} \right) \times 100\% = 13.97\% \]

这意味着该模型的预测结果相对于真实值来说，偏差率约为13.97%。通过这个案例，我们可以看到RSD%在评估模型预测能力方面的具体应用。

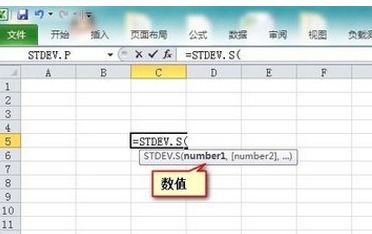
六、Excel中的计算

在Excel中，计算RSD%的过程变得更加简单。可以使用内置的AVERAGE和STDEV函数来计算平均值和标准偏差，然后通过公式计算出RSD%。具体步骤如下：

1. 输入基础数据。

2. 使用AVERAGE函数计算算术平均值。

3. 使用STDEV或STDEV.P函数计算标准偏差（注意：STDEV基于样本，STDEV.P基于总体，根据需求选择合适的函数）。

4. 在另一个单元格中输入公式“=(STDEV(数据范围)/AVERAGE(数据范围))*100”，得到RSD%的值。

七、总结

RSD%作为一个重要的统计指标，通过标准偏差与平均值的比值来衡量数据的离散程度和模型的预测精度。通过计算RSD%，我们可以了解数据点的变异程度、评估模型的稳定性以及比较不同数列的变异程度。无论是在数据分析、科学研究还是模型预测中，RSD%都发挥着不可或缺的作用。因此，掌握RSD%的计算方法和应用具有重要意义。希望本文能够帮助读者更好地理解RSD%的计算和应用，并在实际工作中加以运用。