揭秘：AXA的数值之谜，究竟等于多少？

在日常生活中，我们经常会遇到数学计算，尤其是当涉及到平方这个概念时，“axa等于多少呀”这个问题就显得格外常见。不论是在学习数学的课堂上，还是在解决实际问题的过程中，平方运算都是基础而重要的。那么，今天我们就来详细探讨一下“axa等于多少呀”这个问题，以及与之相关的各个方面，希望能帮助大家更好地理解平方运算。

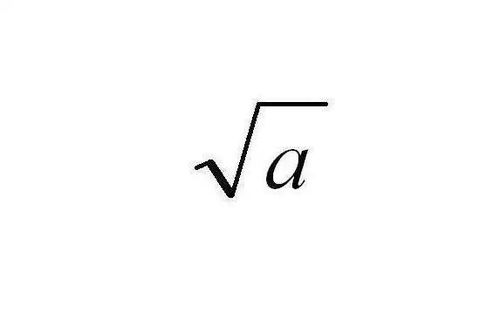
首先，我们得明确什么是平方。简单来说，平方就是一个数与自己相乘的结果。用数学表达式表示就是：如果有一个数a，那么它的平方就是a乘以a，写作a²，也就是“axa”。这里的“²”表示平方的意思，它告诉我们这个数字被乘以了自己一次。

那么，“axa等于多少呀”这个问题，实际上就是在问a的平方是多少。这个答案取决于a的具体值。比如，如果a是2，那么axa就等于2²，也就是2乘以2，结果是4。同样地，如果a是3，那么axa就等于3²，即3乘以3，结果是9。所以，要回答“axa等于多少呀”这个问题，我们必须知道a的具体数值。

接下来，我们来看一些平方运算的基本性质。这些性质有助于我们更深入地理解平方运算，并在实际应用中更加灵活地运用它。

1. 任何数的平方都是非负的：这是平方运算的一个基本性质。因为无论正数还是负数，当它们与自己相乘时，结果总是正的（零的平方也是零，属于非负范畴）。例如，(-3)²等于9，（+3）²也等于9，而0²等于0。

2. 平方运算具有对称性：即a²和(-a)²的值是相同的。这反映了平方运算在数值上不考虑正负的特性。例如，4²和(-4)²都等于16。

3. 平方根运算与平方运算互为逆运算：如果一个数的平方等于b，那么这个数就叫做b的平方根。例如，如果a²=16，那么a可以是4或-4，因为4²和(-4)²都等于16。但需要注意的是，在实数范围内，正数的平方根通常指正的那个数（除非特别说明是负的平方根）。

了解了平方运算的基本性质后，我们再来看看它在实际生活中的应用。平方运算在数学、物理、工程等多个领域都有着广泛的应用，是许多计算的基础。

在数学领域，平方运算经常出现在代数、几何等分支中。例如，在解一元二次方程时，我们需要用到平方根来求解；在几何中，计算正方形的面积时，我们直接用到边长的平方。

在物理领域，平方运算同样扮演着重要角色。例如，在力学中，物体的动能与其速度的平方成正比；在电磁学中，点电荷产生的电场强度与距离的平方成反比。这些关系都体现了平方运算在描述物理现象时的关键作用。

在工程领域，平方运算也经常被用来进行设计和计算。例如，在建筑设计中，计算结构的承重能力时，需要考虑到材料强度的平方关系；在通信工程中，计算信号的强度时，也需要用到平方运算来反映信号的功率变化。

此外，平方运算还在计算机科学、经济学等多个领域有着广泛的应用。在计算机科学中，平方运算被用来进行数据加密、图像处理等；在经济学中，平方运算则被用来计算方差、协方差等统计量，以评估数据的波动性和相关性。

那么，如何快速准确地计算一个数的平方呢？除了直接相乘外，我们还可以利用一些技巧和方法来简化计算过程。

1. 利用平方表：在数学课本或参考资料中，通常会附有平方表，列出了常见整数的平方值。我们可以利用这个表来快速查找和验证计算结果。

2. 利用平方的性质进行估算：对于不是整数的数，我们可以先找到与它接近的整数，然后利用平方的性质进行估算。例如，要计算5.2的平方，我们可以先找到5和6这两个整数，并计算它们的平方值（分别是25和36），然后根据5.2与这两个整数的距离进行适当调整。

3. 利用计算器或计算机程序：现代科技为我们提供了便捷的计算工具。我们可以利用计算器或编写计算机程序来快速准确地计算任何数的平方。

综上所述，“axa等于多少呀”这个问题实际上是在询问一个数的平方值。要回答这个问题，我们需要知道a的具体数值，并了解平方运算的基本性质和应用场景。通过学习和掌握这些知识和技能，我们可以更好地理解和运用平方运算来解决实际问题。无论是在学习数学的课堂上，还是在解决实际问题的过程中，平方运算都将是我们的得力助手。希望这篇文章能帮助大家更好地理解“axa等于多少呀”这个问题及其相关知识。