探索与构建三阶幻方的规律及技巧
三阶幻方的规律和方法

幻方,也称魔方阵或拉丁方阵,是一种将数字排列成方阵的形式,使得方阵中每一行、每一列以及对角线上的数字之和都相等。其中,三阶幻方是最简单也是最常见的一种幻方,它使用1到9的数字排列成一个3x3的方阵,使得方阵的每一行、每一列以及两条对角线上的数字之和均为15。

三阶幻方的构造方法
三阶幻方的构造方法有多种,下面介绍几种常见且易于理解的方法:

方法一:Siamese方法(暹罗法)
这是构造三阶幻方的一种经典方法,步骤如下:
1. 排列数字:将1到9的数字按从左到右、从上到下的顺序排列成一个3x3的矩阵。
```
1 2 3
4 5 6
7 8 9
```
2. 移动数字:将位于第一行的数字向右上方移动(如果超出边界,则移到对应行的左侧)。
将1向右上方移动到第一列第二行的位置(即与2交换位置)。
将2继续向右上方移动到第一列第三行的位置(与3交换位置)。
将3继续向右上方移动,但此时会超出第一列,所以将其移动到第三列第一行的位置(与7交换位置)。
依次类推,直到所有数字都按规则移动完毕。
按照这个方法移动后,得到的幻方如下:
```
8 1 6
3 5 7
4 9 2
```
方法二:对角线法
这种方法通过填充对角线来构造幻方:
1. 填充对角线:将数字1放在第一行中间的位置,然后依次将数字放在其右上方(如果超出边界,则移到下一行的左侧)的位置,直到填满对角线上的三个数字。
```
x 1 x
x x x
x x x
```
然后,将1右上方的位置(第二行第一列)作为第二条对角线的起点,依次填充数字。
2. 补充剩余数字:在填充了两条对角线之后,剩余的四个位置按照从小到大的顺序填充剩下的数字。
得到的幻方如下:
```
2 7 6
9 5 1
4 3 8
```
方法三:奇数阶幻方的通用构造法(Siamese方法的推广)
对于奇数阶的幻方(如3x3、5x5等),可以使用一种通用的构造方法,这里以三阶幻方为例说明:
1. 生成初始矩阵:生成一个n×n(n为奇数)的矩阵,并将1到n²的数字按从左到右、从上到下的顺序填入矩阵中。
2. 确定移动规则:将位于第一行的数字向右上方移动,移动规则如下:
如果目标位置在当前行的右侧,则直接交换;
如果目标位置超出当前行的右侧边界,则将其移动到下一行的最左侧(即第一列);
如果当前行是最后一行且目标位置超出边界,则将其移动到第一行的最左侧(即第一列)。
3. 应用移动规则:按照上述规则,依次将第一行的每个数字向右上方移动,直到所有数字都按规则移动完毕。
对于3x3的幻方,这种方法得到的幻方与Siamese方法得到的幻方相同。
三阶幻方的性质
三阶幻方不仅具有幻方的一般性质(即每一行、每一列以及对角线上的数字之和相等),还具有一些独特的性质:
1. 中心对称性:将三阶幻方绕中心点(即中心元素5)旋转180度后,得到的方阵与原方阵完全相同。
2. 反对角线性质:除了两条主对角线(即从左上角到右下角和从右上角到左下角的对角线)上的数字之和为15外,两条反对角线(即从左上角到左下角的对角线和从右上角到右下角的对角线)上的数字之和也为15(但需要注意的是,对于三阶幻方来说,两条反对角线实际上是重合的,所以这一性质在三阶幻方中并不明显;但在更高阶的奇数阶幻方中,这一性质会更加明显)。
3. 数字分布均匀:在三阶幻方中,每个数字都只出现一次,且每个数字都与其他两个数字相邻(无论是水平、垂直还是对角线方向)。
三阶幻方的应用
1. 数学研究:三阶幻方是组合数学和数论研究中的重要对象之一。通过研究三阶幻方的构造方法和性质,可以推导出更高阶幻方的构造方法和性质。
2. 计算机科学:在计算机科学中,三阶幻方可以用于生成随机数、设计加密算法等。由于其独特的性质和结构,使得幻方在信息安全领域具有潜在的应用价值。
3. 密码学:幻方在密码学中有着悠久的历史和广泛的应用。通过将明文中的字符映射到幻方中的位置,并利用幻方的对称性和均匀性等特点进行加密和解密操作,可以实现一种简单而有效的加密方法。
4. 游戏设计:三阶幻方还可以用于设计一些益智游戏或数学游戏。例如,可以设计一款游戏要求玩家通过移动数字来构造一个合法的三阶幻方;或者设计一款数学游戏来测试玩家对幻方性质和构造方法的理解程度。
综上所述,三阶幻方不仅具有优美的数学结构和独特的性质,还在多个领域有着广泛的应用价值。通过学习和掌握三阶幻方的构造方法和性质,我们可以更好地理解数学中的组合和排列问题,并发现更多有趣的应用场景。
- 上一篇: 揭秘“8023”背后的浪漫含义
- 下一篇: 碧玉植物养殖技巧与养护注意事项概览
-
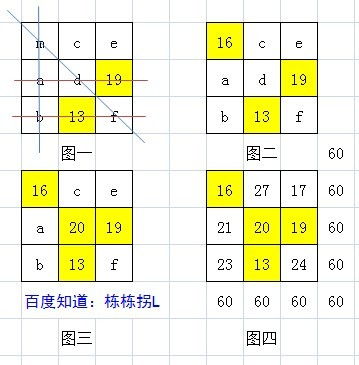 揭秘三阶幻方的神奇规律资讯攻略11-21
揭秘三阶幻方的神奇规律资讯攻略11-21 -
 七步速成:轻松图解还原三阶魔方秘籍资讯攻略12-01
七步速成:轻松图解还原三阶魔方秘籍资讯攻略12-01 -
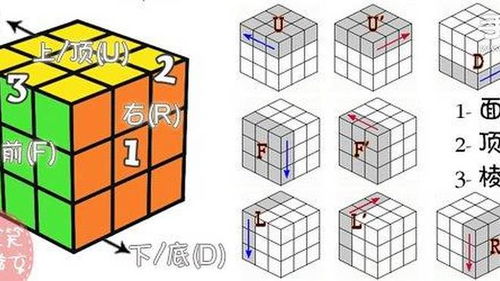 三阶魔方速成秘籍:白话图解,手把手带你玩转魔方!资讯攻略11-06
三阶魔方速成秘籍:白话图解,手把手带你玩转魔方!资讯攻略11-06 -
 三阶魔方速成:简单快速还原技巧图解指南资讯攻略11-21
三阶魔方速成:简单快速还原技巧图解指南资讯攻略11-21 -
 广东高考作文:审题技巧、立意构建及范文解析点评资讯攻略04-02
广东高考作文:审题技巧、立意构建及范文解析点评资讯攻略04-02 -
 三阶魔方复原全攻略:解锁第三步秘籍资讯攻略10-28
三阶魔方复原全攻略:解锁第三步秘籍资讯攻略10-28












