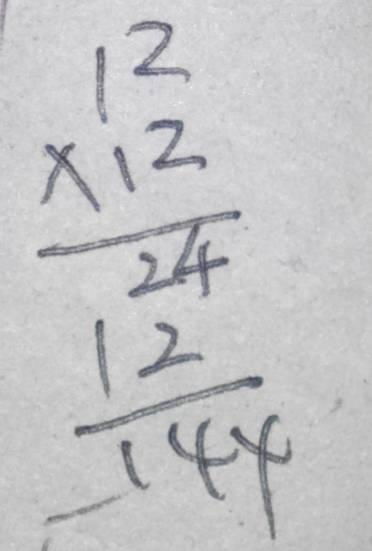揭秘12x12的超速心算技巧
在这个数字主导的时代,快速而准确地完成数学计算不仅关乎学习效率,更是职场和生活中不可或缺的技能。今天,我们就来揭秘一个简单却高效的计算技巧——“12x12的快速算法”,让你在分秒必争的情况下也能轻松驾驭乘法运算,成为朋友圈中的数学小达人!

揭开神秘面纱:为何选择12x12?
在数学学习的征途中,乘法表是基础中的基础。而12这个数字,既非个位数那般简单直白,也不像两位数中的大数那样令人望而生畏,它恰好站在了一个微妙的平衡点上。掌握12x12的快速算法,不仅能提升你的计算速度,还能为更高阶的数学问题打下坚实的基础。毕竟,在日常生活和工作中,涉及12的乘法运算无处不在,从时间的计算到物品的打包,再到分数的简化,12都是一个高频出现的数字。

快速算法揭秘:三步走战略
第一步:分解与重组
面对12x12这样的乘法,最直观的方法是直接相乘,但这样的方法虽然准确,却不够快捷。快速算法的核心在于“分解与重组”。我们可以将12拆分为10+2,这样,12x12就变成了(10+2)x(10+2)。
第二步:应用分配律
接下来,利用乘法分配律,将(10+2)x(10+2)展开为10x10 + 10x2 + 2x10 + 2x2。这一步看似复杂,实则是将一个大问题拆解成了四个小问题,每个小问题都更加容易解决。
第三步:快速求和
现在,我们只需分别计算这四个小问题的结果,并将它们相加即可。10x10等于100,10x2等于20,2x10也等于20(注意到这里有两个相同的项,可以迅速相加),最后2x2等于4。将这些结果相加:100 + 20 + 20 + 4 = 144。
看,通过分解、分配、求和这三步,我们就快速而准确地得出了12x12的答案——144!
深入剖析:背后的逻辑与优势
这种快速算法之所以高效,是因为它充分利用了数学的基本法则,将复杂的计算过程简化为一系列简单的步骤。它不仅适用于12x12,还可以推广到任何形如(a+b)x(a+b)的乘法运算中,只要a和b是已知的数字。
逻辑思维训练
更重要的是,这种算法锻炼了你的逻辑思维能力。在分解问题的过程中,你需要思考如何将一个看似复杂的问题转化为几个简单的问题;在分配和求和时,你又需要保持高度的注意力,确保每个步骤都准确无误。这种训练对于提高解决问题的能力大有裨益。
提升计算效率
在日常生活中,我们经常需要快速做出决策或计算,比如估算购物预算、计算工作效率等。掌握快速算法,意味着你能在更短的时间内得出结果,从而赢得宝贵的时间优势。
增强自信心
每当你成功地运用快速算法解决问题时,都会有一种成就感油然而生。这种成就感会转化为自信,让你在面对数学或其他领域的挑战时更加从容不迫。
实战演练:更多应用案例
为了让你更加熟练地掌握这种快速算法,让我们来看看它在其他乘法运算中的应用。
案例一:13x13
同样地,我们可以将13拆分为10+3,然后应用分配律:(10+3)x(10+3) = 10x10 + 10x3 + 3x10 + 3x3 = 100 + 30 + 30 + 9 = 169。
案例二:15x17
这次我们尝试稍微复杂一点的组合,将15视为10+5,17视为10+7:(10+5)x(10+7) = 10x10 + 10x7 + 5x10 + 5x7 = 100 + 70 + 50 + 35 = 255。
通过这些案例,你可以看到,无论数字大小,只要掌握了分解、分配、求和的基本步骤,就能迅速得出答案。
技巧升级:结合记忆法
为了进一步提高计算速度,你还可以结合记忆法。比如,对于形如(a+b)x(a+b)的运算,你可以记住一个口诀:“头尾相乘是首项,两倍中项加中央,尾项平方放最后。”这个口诀对应了快速算法中的三个步骤:首先计算a的平方(头尾相乘),然后计算两倍ab(两倍中项),最后加上b的平方(尾项平方)。
结语:开启数学新世界的大门
通过今天的学习,我们不仅掌握了12x12的快速算法,还学会了如何将其应用于更广泛的乘法运算中。这不仅仅是一种计算技巧的提升,更是逻辑思维和问题解决能力的飞跃。
现在,当你再次面对乘法运算时,是否会感到更加自信和从容?是否已经开始期待在下一次的数学挑战中大展身手?记住,数学的世界充满了无限可能,只要勇于探索,你总能发现新的惊喜和乐趣。
所以,不妨现在就拿起笔,找几个数字试试身手吧!相信在不久的将来,你会因为掌握了这些快速算法而在数学的世界里游刃有余,开启一段全新的旅程。
- 上一篇: 怎样轻松改变Word文档的字体颜色,让文字更出彩?
- 下一篇: 宝马:源自哪个国家的豪华汽车巨头?
-
 揭秘珠心算可能带来的不良影响资讯攻略03-16
揭秘珠心算可能带来的不良影响资讯攻略03-16 -
 掌握心算加减法,轻松提升计算能力!资讯攻略11-30
掌握心算加减法,轻松提升计算能力!资讯攻略11-30 -
 如何快速致富?揭秘Gangstar IV的超速赚钱秘诀!资讯攻略12-03
如何快速致富?揭秘Gangstar IV的超速赚钱秘诀!资讯攻略12-03 -
 辻洼凛音惊艳亮相!揭秘《最强大脑》第二季她在哪一期闪耀登场资讯攻略03-10
辻洼凛音惊艳亮相!揭秘《最强大脑》第二季她在哪一期闪耀登场资讯攻略03-10 -
 37天将雄狮:超速辅助攻略,轻松升级称霸!资讯攻略11-05
37天将雄狮:超速辅助攻略,轻松升级称霸!资讯攻略11-05 -
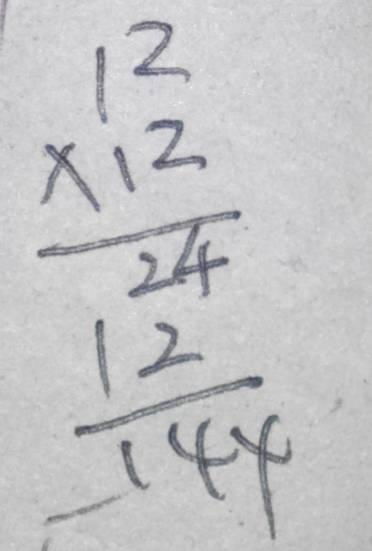 快速计算12乘以12的方法资讯攻略12-07
快速计算12乘以12的方法资讯攻略12-07