如何用尺规作图的方法步骤来作平行线?
在几何学的浩瀚宇宙中,平行线作为基础的几何概念,扮演着举足轻重的角色。它们是在同一平面内,永远不相交的两条直线的代名词,象征着一种永恒的平行与距离之美。尺规作图,作为几何作图的基本方法之一,为我们提供了一种精确而优雅的方式来绘制平行线。本文将多维度地探讨尺规作平行线的步骤,通过不同的方法和原理,带领读者走进这一几何艺术的殿堂。

尺规作平行线的多种探索
方法一:推平行线法
这是利用直尺和三角尺相互配合的经典方法。首先,我们使用三角尺画出一条直线,作为我们的基准线。随后,将直尺的一侧边缘紧贴着三角尺的另一条直角边,确保直尺与三角尺保持固定角度。接着,我们沿着直尺平移三角尺,直至到达一个满意的位置,再用三角尺的斜边画出第二条直线。这条新画出的直线与原先的基准线就是平行线。通过这种方法,我们可以轻松实现直线的平行延伸,精确且直观。

方法二:双三角尺法
双三角尺法同样是一种直观而有效的方法。首先,用三角尺画出一条直线。然后,我们将其中一把三角尺的一条直角边紧靠这条直线,另一把三角尺则紧贴着第一把三角尺的另一条直角边。这样,我们就构建了一个稳定的直角框架。最后,沿着第二把三角尺的直角边画出另一条直线,这条新直线与原直线平行。这种方法利用了三角尺的直角特性,确保了平行线的精确性。

方法三:量角器法
量角器的加入,为绘制平行线提供了另一种可能。首先,用直尺画出一条基准线。接着,将量角器的中心与这条直线的一个端点重合,零刻度线也与直线重合。然后,在量角器上找到要画的另一条直线的一个端点的刻度,并在这个刻度上标记一个点。最后,连接这两个点,得到的新直线与原直线平行。这种方法利用了量角器的精确测量功能,使得平行线的绘制更加严谨。
方法四:几何定理法
除了直接的作图工具,我们还可以借助几何定理来构造平行线。例如,通过圆规和直尺的结合,我们可以实现这一目的。首先,画一条直线l和一个点P,点P不在直线l上。以点P为圆心,任意长度为半径画圆,与直线l交于点A和B。接着,以点A为圆心,AB为半径画圆,以点B为圆心,AB为半径画圆,两圆交于点C。最后,连接点P和点C,得到的直线PC即为平行于直线l的平行线。这一方法的原理在于,直线l和直线PC被直线PA和直线PB所截,形成的同位角相等,因此两直线平行。
另一种几何定理法是通过构造内错角或同旁内角来实现平行线的绘制。例如,画一条直线l和一点P,点P不在直线l上。过点P画一条直线m与直线l相交于点A。以点A为圆心,任意长度为半径画圆,与直线l交于点B,与直线m交于点C。以点C为圆心,AC为半径画圆,与直线m交于点D。连接点P和点D,得到的直线PD即为平行于直线l的平行线。这一方法的原理在于,直线l和直线PD被直线m所截,形成的内错角相等,因此两直线平行。
方法五:利用垂线与平行线性质
我们还可以利用平行线的性质来绘制平行线。在已知直线上取两点,分别作两条与已知直线垂直的线段,这两条线段就是已知直线的垂线。然后,用直尺连接这两条垂线的另一端点,得到的新直线与已知直线平行。这种方法基于平行线的一个重要性质:过直线外一点,有且仅有一条直线与这条直线平行。
方法六:尺规结合法
通过尺规结合,我们还可以探索更多绘制平行线的方法。例如,用圆规在纸上画一个已知半径的圆,然后用直尺的一边紧靠圆的边缘,并在圆上任取一点。接着,用直尺的另一边紧靠已知直线并在已知直线上任取一点。最后,用圆规在这两点之间画一条直线,这条直线与已知直线平行。这一方法虽然稍显复杂,但它同样有效地利用了尺规作图的基本原理。
方法七:现代技术法
在数字化时代,我们还可以借助电脑绘图软件来绘制平行线。使用绘图软件如画图板、Photoshop等,我们可以直接利用工具画出平行线。这些软件通常提供了绘制直线和平行线的工具,用户只需按照软件的指示进行操作即可。这种方法不仅快捷高效,而且能够实现高度的精确度和灵活性。
平行线的应用与启示
平行线不仅是几何学中的基本概念,它们还广泛应用于建筑设计、工程设计、物理学等多个领域。在建筑设计中,平行线的应用确保了建筑结构的稳定性和美观性;在工程设计中,平行线的绘制有助于工程师实现精确的测量和布局;在物理学中,平行线的概念则帮助我们理解光线、磁场等自然现象的传播规律。
此外,平行线还蕴含着深刻的哲学意义。它们象征着一种永恒的平行与距离之美,提醒我们,在某些情况下,保持一定的距离和独立,反而能够实现更好的和谐与共存。这正如人与人之间的交往,适当的距离和尊重,往往能够增进彼此的理解和友谊。
结语
尺规作平行线,不仅是一种几何作图技巧,更是一种思维方式和探索精神的体现。通过不同的方法和原理,我们可以发现平行线的多样性和魅力。在未来的学习和生活中,让我们继续探索平行线的奥秘,发掘它更多的应用价值,让我们的生活更加美好和充实。正如几何学中的平行线一样,让我们在人生的道路上,保持独立与和谐,共同创造更加美好的未来。
- 上一篇: 淘宝人生账单查看方法是什么?
- 下一篇: 打造卓越政法干警:必备素质与成长指南
-
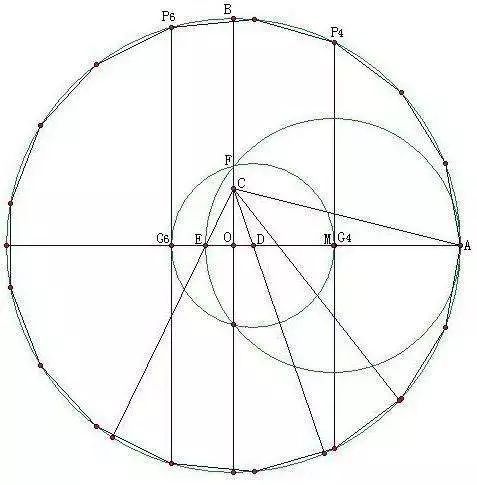 高斯如何作出正十七边形?资讯攻略02-01
高斯如何作出正十七边形?资讯攻略02-01 -
 七巧板拼长方形的步骤与方法资讯攻略10-27
七巧板拼长方形的步骤与方法资讯攻略10-27 -
 如何用一副七巧板拼出一个长方形?资讯攻略10-28
如何用一副七巧板拼出一个长方形?资讯攻略10-28 -
 如何用七巧板拼成一个长方形?资讯攻略10-28
如何用七巧板拼成一个长方形?资讯攻略10-28 -
 如何用七巧板拼出数字6?资讯攻略12-04
如何用七巧板拼出数字6?资讯攻略12-04 -
 如何用七巧板拼出一个长方形?资讯攻略10-28
如何用七巧板拼出一个长方形?资讯攻略10-28












