同类项的定义及详细概念解析
在数学的世界里,我们常常会遇到各种各样的数学术语和概念,其中“同类项”就是一个既基础又重要的概念。无论你是小学生刚开始接触数学,还是中学生、大学生在深入学习代数,掌握同类项的定义与概念都将帮助你更好地理解和解决数学问题。那么,同类项的定义与概念到底是什么呢?让我们一起慢慢揭开它的面纱。

首先,同类项这个概念主要出现在代数运算中,特别是当我们需要对式子进行合并同类项时。想象一下,你有一堆苹果和一堆香蕉,当你想要知道总共有多少水果时,你会怎么做?没错,你需要把苹果和苹果加在一起,香蕉和香蕉加在一起,然后再把两者的总数相加。同样地,在代数中,我们也需要把相同类型的项(即同类项)放在一起进行运算。

同类项的定义
同类项,简而言之,就是所含的字母相同,并且相同字母的指数也相同的单项式。这里的“单项式”指的是一个或多个数与字母的乘积,比如5x、3y²、2ab等。

1. 所含字母相同:这意味着两个或多个单项式中都包含相同的字母。比如x和2x,它们都包含字母x。

2. 相同字母的指数相同:指数是字母右上角的数字,用来表示该字母需要被乘多少次。如果两个单项式中的相同字母的指数不同,那么它们就不是同类项。比如x²和x³,虽然它们都包含字母x,但x的指数不同,所以它们不是同类项。
同类项的例子
为了更好地理解同类项的概念,我们可以看一些具体的例子:
3x和5x:这两个单项式都包含字母x,且x的指数都是1(虽然1通常不写出来),所以它们是同类项。
2y²和-4y²:这两个单项式都包含字母y,且y的指数都是2,所以它们也是同类项。
7ab和-3ab:这两个单项式都包含字母a和b,且a和b的指数都是1(不写出来),所以它们也是同类项。
4x²y和-2x²y³:虽然这两个单项式都包含字母x和y,但y的指数不同(一个是1,一个是3),所以它们不是同类项。
同类项的作用
同类项在数学中的作用主要体现在代数式的化简和运算上。通过合并同类项,我们可以使代数式更加简洁明了,从而更容易看出其中的数学关系和规律。
1. 化简代数式:合并同类项是化简代数式的重要手段。比如,对于代数式3x+5x-2x,我们可以将3x、5x和-2x这三项合并成6x-2x,再进一步化简为4x。这样,代数式就变得更加简洁了。
2. 求解方程:在解方程时,我们也需要用到合并同类项的技巧。比如,在方程2x+3=7x-5中,我们可以通过将2x和-7x合并成-5x,将常数项3和-5合并成-2,从而得到-5x=-2,进而求解出x的值。
3. 理解数学关系:合并同类项还可以帮助我们更好地理解数学关系。比如,在多项式函数中,同类项的系数可以表示函数的某些特性(如开口方向、顶点坐标等)。通过合并同类项,我们可以更直观地看出这些特性。
如何合并同类项
合并同类项的过程其实非常简单,只需要将同类项的系数相加或相减,而保持字母和指数不变即可。下面是一个具体的步骤:
1. 识别同类项:首先,我们需要仔细阅读代数式,找出其中的同类项。
2. 列出同类项:将找出的同类项列在一起,方便进行下一步的运算。
3. 计算系数和:将同类项的系数相加或相减,得到新的系数。如果同类项有多个,可以依次相加或相减。
4. 写出结果:将新的系数与原来的字母和指数组合在一起,得到合并后的代数式。
例如,对于代数式3x+5x-2x+4y-3y,我们可以按照以下步骤进行合并同类项:
识别同类项:3x、5x和-2x是同类项;4y和-3y是同类项。
列出同类项:3x+5x-2x;4y-3y。
计算系数和:3x+5x-2x=(3+5-2)x=6x;4y-3y=(4-3)y=y。
写出结果:6x+y。
同类项在生活中的应用
虽然同类项是一个
- 上一篇: 如何在人人影视上观看剧集?
- 下一篇: 揭秘!我国古代的“茶圣”究竟是谁?蚂蚁庄园揭晓答案
-
 初一数学:同类项定义及合并方法资讯攻略10-28
初一数学:同类项定义及合并方法资讯攻略10-28 -
 同类项的定义及识别资讯攻略11-03
同类项的定义及识别资讯攻略11-03 -
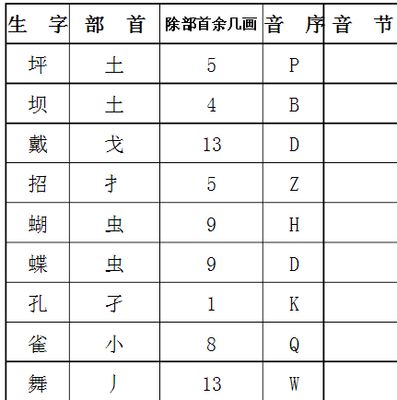 音节与音序的区别及音序定义资讯攻略11-09
音节与音序的区别及音序定义资讯攻略11-09 -
 商品的使用价值定义及解析资讯攻略11-22
商品的使用价值定义及解析资讯攻略11-22 -
 孤品定义及含义解析资讯攻略11-06
孤品定义及含义解析资讯攻略11-06 -
 职业年金定义及解析资讯攻略11-21
职业年金定义及解析资讯攻略11-21












