屈服极限的计算公式是什么?
屈服极限计算公式深度解析

在材料科学与工程领域,屈服极限(或称屈服强度)是一个至关重要的力学性能指标。它反映了材料在受到外力作用时,从弹性变形阶段过渡到塑性变形阶段的临界点。了解屈服极限,对于材料的选用、结构设计、制造工艺及安全评估等方面都具有重要意义。本文将深入探讨屈服极限的定义、分类以及计算公式,为读者提供一个全面而直接的知识体系。

一、屈服极限的定义
屈服极限,是指在拉伸试验中,试样在承受拉力过程中,应力不增加(或略有减小)而试样仍能继续伸长时的应力值。此时,材料开始发生显著的塑性变形,标志着弹性阶段的结束和塑性阶段的开始。在应力-应变曲线上,屈服极限对应的是屈服点或屈服平台。根据屈服点的表现形式,屈服极限可分为上屈服强度和下屈服强度。

上屈服强度(ReH):在应力-应变曲线上,试样发生屈服而力首次下降前的最大应力值。由于上屈服强度受试样形状、尺寸、试验机刚度及加载速度等因素的影响较大,其值往往不够稳定,因此在实际应用中较少采用。

下屈服强度(ReL 或 Rp0.2):在应力-应变曲线上,不计初始瞬时效应时的最小应力值。通常规定,以产生0.2%残余变形的应力值作为下屈服强度。下屈服强度较为稳定,重复性好,是工程上常用的屈服极限指标。
二、屈服极限的分类
屈服极限根据材料的种类、试验条件及测定方法的不同,可分为多种类型,包括但不限于:
条件屈服强度:指在一定试验条件下测得的屈服强度,如室温拉伸试验中的下屈服强度。
真屈服强度:在理想情况下,材料内部应力分布均匀且不考虑试样尺寸效应时的屈服强度。真屈服强度往往难以直接测得,但可通过理论计算或数值模拟得到。
持久屈服强度:在高温长期载荷作用下,材料抵抗塑性变形的能力。持久屈服强度是高温结构材料的重要性能指标。
塑性屈服强度:在特定塑性变形量下对应的应力值,如上文提到的下屈服强度即为塑性屈服强度的一种。
弹性屈服强度:材料在弹性范围内即将进入塑性变形阶段时的应力值。然而,严格来说,弹性屈服强度并不是一个明确的界限,因为弹性与塑性变形之间存在一定的过渡区域。
三、屈服极限的计算公式
1. 拉伸试验法
对于大多数金属材料而言,屈服极限主要通过拉伸试验来测定。拉伸试验是在标准试样上施加轴向拉伸力,直至试样断裂,同时记录应力-应变曲线的全过程。在应力-应变曲线上,可以直接读取或计算得到屈服极限。
下屈服强度(Rp0.2):通过测量试样在拉伸过程中产生0.2%残余变形时的应力值来确定。计算公式为:
\[Rp0.2 = \frac{F_{0.2}}{A_0}\]
其中,\(F_{0.2}\)为产生0.2%残余变形时的拉力,\(A_0\)为试样的原始截面积。
上屈服强度(ReH):虽然上屈服强度在实际工程中应用较少,但其计算方法同样基于应力-应变曲线。通常,通过寻找应力-应变曲线上首次出现下降趋势的点,并读取该点的应力值作为上屈服强度。需要注意的是,由于上屈服强度的测定受多种因素影响,因此其值往往不够稳定。
2. 理论计算法
对于某些特定材料或结构,屈服极限也可以通过理论计算得到。这种方法通常基于材料的微观结构、化学成分、加工硬化特性等因素,结合弹塑性力学的基本原理进行推导。然而,由于材料性能的复杂性,理论计算法往往难以得到精确的结果,且计算过程繁琐。因此,在实际应用中,理论计算法通常作为拉伸试验法的补充或验证手段。
3. 经验公式法
对于一些常用的材料,如钢材、铝合金等,研究人员已经通过大量的试验数据积累,建立了屈服极限与材料成分、加工状态等参数之间的经验公式。这些经验公式可以在一定程度上预测材料的屈服极限,为材料选用和结构设计提供参考。但需要注意的是,经验公式法的准确性往往受到材料种类、试验条件及数据样本量的限制。
4. 数值模拟法
随着计算机技术的飞速发展,数值模拟法已经成为研究材料屈服极限的重要手段之一。通过有限元分析、分子动力学模拟等方法,可以模拟材料在拉伸过程中的应力-应变行为,进而计算得到屈服极限。数值模拟法具有成本低、效率高、可重复性好等优点,尤其适用于复杂结构或新材料的研究。但需要注意的是,数值模拟法的准确性取决于模型的建立、参数的选取以及算法的优化等因素。
四、屈服极限的应用
屈服极限作为材料力学性能的重要指标之一,在多个领域具有广泛的应用。在机械设计中,屈服极限是选择材料、确定零件尺寸和校核强度的重要依据;在材料开发中,屈服极限是评价材料性能优劣的关键指标之一;在结构分析中,屈服极限是评估结构安全性的重要参数;在工艺制定中,屈服极限是制定热处理、锻造、轧制等工艺参数的重要依据。
综上所述,屈服极限的计算公式及其应用是材料科学与工程领域的重要研究内容。通过深入了解屈服极限的定义、分类及计算方法,可以为材料的选用、结构设计、制造工艺及安全评估等方面提供有力的技术支持。同时,随着科学技术的不断进步,新的计算方法和技术手段不断涌现,将进一步推动屈服极限研究的发展和应用。
- 上一篇: 如何深入分析进化树
- 下一篇: 188号段所属运营商是哪家
-
 资料分析中的比重计算公式是什么?资讯攻略11-08
资料分析中的比重计算公式是什么?资讯攻略11-08 -
 正方形周长的计算公式是什么资讯攻略11-01
正方形周长的计算公式是什么资讯攻略11-01 -
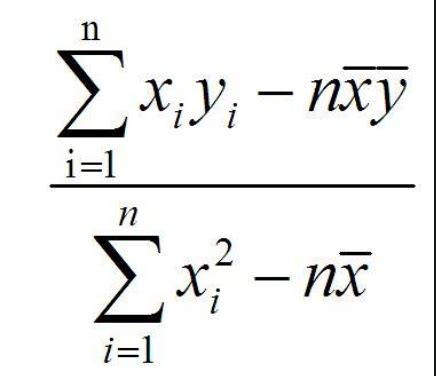 回归分析法的计算公式是什么?资讯攻略12-01
回归分析法的计算公式是什么?资讯攻略12-01 -
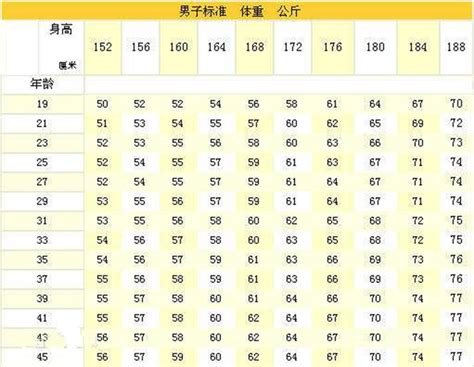 中考时计算身高与体重的公式是什么?资讯攻略11-23
中考时计算身高与体重的公式是什么?资讯攻略11-23 -
 揭秘:辨别真假铍铜的实用技巧资讯攻略11-05
揭秘:辨别真假铍铜的实用技巧资讯攻略11-05 -
 半圆面积的计算公式是什么?资讯攻略10-29
半圆面积的计算公式是什么?资讯攻略10-29