正数和负数分别是如何定义的?
在数学领域中,正数与负数是两个核心概念,它们共同构成了数轴上的基本元素,为我们理解和处理数量、方向、变化等提供了有力的工具。首先,我们需要明确正数和负数的定义,以及它们在数学和现实生活中的应用。
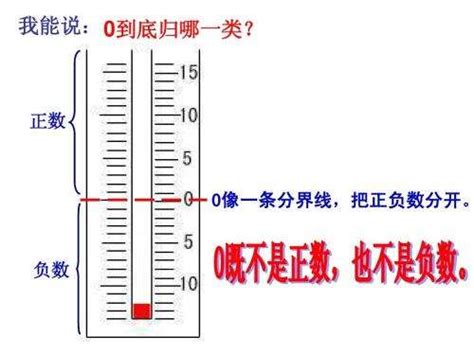
正数的定义相对直观,它表示大于零的数。在数轴上,正数位于零点的右侧,随着数值的增加,点向右移动。正数在生活中无处不在,比如我们的收入、年龄、温度(在摄氏度表示中,零度以上的温度)、海拔高度(相对于海平面以上)等,都可以用正数来表示。正数具有加法、减法、乘法和除法等基本运算性质,这些运算遵循数学中的基本法则,如加法交换律、结合律,乘法分配律等。

与正数相对应的是负数,它表示小于零的数。在数轴上,负数位于零点的左侧,随着数值的减小(或者说绝对值的增加),点向左移动。负数在现实生活中同样有着广泛的应用,比如我们的支出(相对于收入而言)、温度的下降(在摄氏度表示中,零度以下的温度)、海拔高度的下降(相对于海平面以下)、负债等,都可以用负数来表示。负数的运算同样遵循数学中的基本法则,但需要注意的是,负数的乘法运算结果的正负取决于两个乘数的符号,即“同号得正,异号得负”。

正数和负数在数学中不仅仅是简单的数字符号,它们还承载着丰富的数学意义和几何意义。在数轴上,正数和负数分别位于零点的两侧,形成了对称的结构。这种对称性在数学中有着重要的应用,比如在对称性质的研究、方程的求解等方面。同时,正数和负数还可以用来表示方向,比如在平面直角坐标系中,正数表示向右或向上的方向,负数则表示向左或向下的方向。这种方向性的表示方法在计算几何、物理问题等方面有着广泛的应用。

除了数学意义外,正数和负数还具有重要的实际应用价值。在商业领域,正数和负数可以用来表示收入和支出,帮助我们更好地管理财务。在科学领域,正数和负数可以用来表示温度的变化、海拔高度的升降等自然现象,为我们提供了理解和预测这些现象的工具。在工程领域,正数和负数可以用来表示力的大小和方向、电压的正负极等,对于设计和优化工程系统具有重要的意义。

此外,正数和负数在数学中还涉及到许多重要的概念和定理。比如绝对值的概念,它表示一个数到零点的距离,无论是正数还是负数,其绝对值都是非负的。绝对值的运算性质在解决许多数学问题中都有着重要的作用。再比如有理数和无理数的概念,它们都是基于正数和负数的定义而得出的。有理数是可以表示为两个整数之比的数,而无理数则是不能表示为两个整数之比的数。有理数和无理数在数学中有着不同的性质和运算规则,但它们都包含了正数和负数的元素。
在代数中,正数和负数更是无处不在。方程的求解、不等式的判断、函数的定义和性质等都与正数和负数密切相关。比如一元一次方程的求解过程中,就需要判断系数的正负来确定方程的解的方向。在不等式的判断中,正数和负数的符号变化直接影响着不等式的解集。在函数的定义中,正数和负数可以用来表示函数的增减性、极值等性质。
在几何学中,正数和负数也有着重要的应用。比如在平面直角坐标系中,正数和负数可以用来表示点的坐标、向量的方向和长度等。在解析几何中,通过引入正数和负数的概念,我们可以将几何问题转化为代数问题来解决,从而大大简化了问题的求解过程。
总的来说,正数和负数是数学中不可或缺的基本元素。它们不仅在数学理论中有着重要的地位和作用,还在实际应用中发挥着巨大的作用。通过学习和掌握正数和负数的定义、性质以及运算规则等基础知识,我们可以更好地理解和运用数学工具来解决实际问题。同时,正数和负数的概念也为我们提供了一种全新的思维方式和解决问题的方法论启示即要全面、辩证地看待问题不仅要看到事物的正面和积极面还要看到事物的反面和消极面从而更加全面、准确地把握事物的本质和规律。
因此,在学习数学的过程中我们应该充分重视正数和负数的概念及其相关知识的学习和应用不断提高自己的数学素养和思维能力为更好地解决实际问题打下坚实的基础。同时我们也应该保持对数学的敬畏之心不断探索数学的奥秘和魅力为人类的进步和发展贡献自己的力量。
- 上一篇: 揭秘!史前巨兽:重达两吨的古巨龟领衔十大巨型动物祖先
- 下一篇: 精通PS:揭秘通道抠图的神奇步骤
-
 负数到底是什么?了解它背后的意义!资讯攻略02-06
负数到底是什么?了解它背后的意义!资讯攻略02-06 -
 根号5的计算方法及结果是多少资讯攻略12-03
根号5的计算方法及结果是多少资讯攻略12-03 -
 五谷中稻、麦、黍、菽、稷的读音分别是什么?资讯攻略11-03
五谷中稻、麦、黍、菽、稷的读音分别是什么?资讯攻略11-03 -
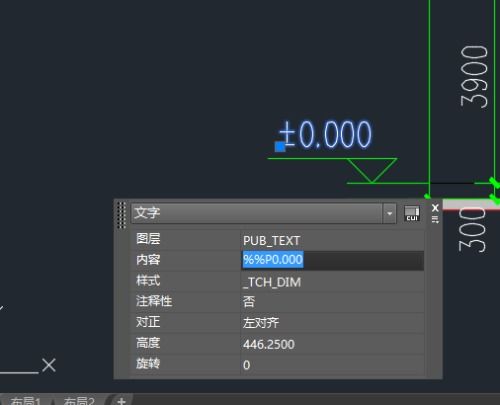 如何输入正负零符号资讯攻略11-22
如何输入正负零符号资讯攻略11-22 -
 Excel技巧:轻松设置绝对值公式的步骤资讯攻略11-03
Excel技巧:轻松设置绝对值公式的步骤资讯攻略11-03 -
 What Does ±0 Mean?资讯攻略11-22
What Does ±0 Mean?资讯攻略11-22










