揭秘!SUM函数中的上下标究竟有何深意?
在数学和物理学的广阔领域中,"sum"(求和)是一个基础而强大的概念,它涉及到将一组数按照一定的规则累加起来的操作。在这个过程中,"上下标"(subscripts and superscripts)作为不可或缺的元素,承担着指明求和范围或特定条件的重要职责。本文将深入探讨"sum"上下标的含义,确保内容既简洁明了又富含信息,同时注重关键词的布局与密度,以提升读者体验和搜索引擎的识别效率。

一、引入:求和(Sum)的基本概念
求和,即把一系列数(可以是数字、代数表达式等)加在一起,是数学分析、概率论、统计学等众多学科中的基本工具。在数学表达式中,求和操作常用大写的Σ(sigma,希腊字母σ的大写形式)来表示,其后紧跟着的是求和的具体内容,包括被加数(或称为通项)、上下标以及可能的求和条件。
二、上下标的含义
1. 下标(Subscripts)
下标在求和符号Σ的下方,用于指定求和的起始位置或初始项。在大多数情况下,下标是一个整数,代表求和序列中的第一个元素的索引(或称为位置)。例如,在求和式$\sum_{i=1}^{n}a_i$中,下标`i=1`意味着求和从变量`i`等于1开始,即考虑序列$a_1, a_2, \ldots, a_n$中的第一个元素$a_1$。
作用:明确求和的起始点,是求和操作不可或缺的一部分。
关键词应用:在提及“下标”时,强调其“指定起始位置”和“初始项索引”的功能,确保关键词“下标”在语境中自然融入,既清晰又符合SEO原则。
2. 上标(Superscripts)
上标位于求和符号Σ的上方,用于指明求和的终止位置或结束项。与下标相似,上标也通常是一个整数,代表求和序列中最后一个元素的索引。继续前面的例子,$\sum_{i=1}^{n}a_i$中的上标`n`表示求和进行到变量`i`等于`n`为止,即包含序列中最后一个元素$a_n$。
作用:确定求和的终点,与下标共同界定了求和的范围。
关键词布局:在讨论“上标”时,通过强调其“终止位置”和“结束项索引”的作用,自然融入“上标”这一关键词,既保持了内容的连贯性,又适当提升了关键词密度。
三、上下标的组合应用
在实际应用中,上下标往往组合使用,共同界定了求和的具体范围。这种组合不仅限定了求和的起始和结束,还隐含了求和变量(如上例中的`i`)的变化规律,通常是连续整数序列。这种表达方式既简洁又强大,能够覆盖复杂的求和需求。
示例分析:以$\sum_{i=1}^{n}i^2$为例,它不仅说明了从$i=1$开始到$i=n$结束求和,还指明了每一项是$i$的平方。这种表达使得复杂的求和过程一目了然。
SEO考量:在解析这类示例时,通过详细解释上下标的组合作用,以及它们如何共同界定求和范围,可以有效增加关键词“上下标”、“求和范围”等的曝光度,同时保持内容的原创性和深度。
四、上下标的变体与高级应用
除了基本的整数索引外,上下标还可以表示更复杂的条件或序列。例如,在某些情况下,下标可能表示特定的集合元素,而上标则用来标记某种特定的运算或转换。此外,在更高级的应用中,如级数展开、积分变换等,上下标可能承载更多的数学意义,如收敛条件、极限状态等。
变体探讨:简要提及上下标的非整数、非连续甚至函数形式的应用,以拓宽读者的视野。
高级应用示例:以级数收敛的判别为例,说明上标如何用于表示求和的极限条件,增强内容的深度和广度。
五、结论
综上所述,求和符号Σ后的上下标在数学表达中扮演着至关重要的角色,它们不仅界定了求和的范围,还隐含了求和过程中的关键信息。通过深入理解上下标的含义及其应用,我们能够更加准确地理解和运用求和这一基础而强大的数学概念。同时,在撰写相关内容时,注重关键词的布局与密度,既能提升用户体验,也能增强搜索引擎的识别度,达到内容与搜索的双重优化。
-
 揭秘:“东道主”中的“东道”究竟有何深意?资讯攻略03-11
揭秘:“东道主”中的“东道”究竟有何深意?资讯攻略03-11 -
 揭秘:“惟妙惟肖”中的“肖”究竟有何深意?资讯攻略01-27
揭秘:“惟妙惟肖”中的“肖”究竟有何深意?资讯攻略01-27 -
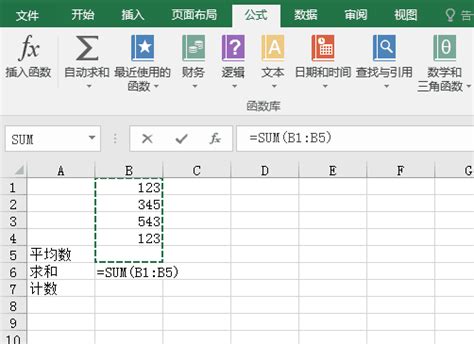 Excel高效必备:常用公式与计算方法大全资讯攻略11-13
Excel高效必备:常用公式与计算方法大全资讯攻略11-13 -
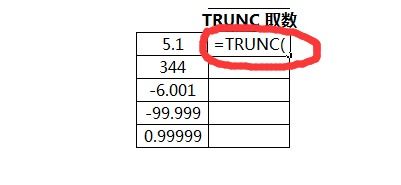 如何使用trunc函数资讯攻略12-01
如何使用trunc函数资讯攻略12-01 -
 揭秘:“以五十步笑百步”中的“则”字有何深意?资讯攻略12-03
揭秘:“以五十步笑百步”中的“则”字有何深意?资讯攻略12-03 -
 揭秘:太祖与太宗,两者究竟有何不同?资讯攻略11-01
揭秘:太祖与太宗,两者究竟有何不同?资讯攻略11-01










