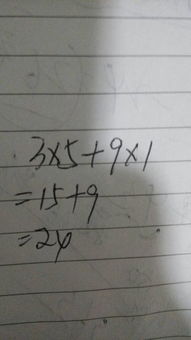如何用1555算出24点,三种方法是什么?
在数学的奇妙世界里,有一种游戏叫做“24点游戏”,它简单却富有挑战性,总能激发人们对数字的无限遐想与探索。今天,我们就来一起揭秘如何用四个数字——1、5、5、5,通过加、减、乘、除四种基本运算,巧妙地组合出24这个结果。这不仅仅是一场数字游戏,更是一次思维的体操,让我们一起踏上这场智慧之旅,探索出三种别出心裁的解法,让你的大脑也来一场精彩的“体操表演”吧!

第一种解法:连环相乘与巧妙相减
想象一下,你手中握有四张数字卡片,分别是1、5、5、5,你的目标是将它们通过运算变成24。让我们先尝试一种直观却又略带技巧性的方法——连环相乘后再进行巧妙的减法运算。
首先,观察这些数字,我们可以发现两个5相乘会得到25,这个数字非常接近我们的目标24,仅仅多出了1。这为我们提供了一个思路:是否可以通过某种方式“借”走这多余的1呢?答案是肯定的,而且方法还不止一种。但在这里,我们要展示的是最直接且富有创意的一种。
将两个5相乘,得到25,这是我们的基础值。接下来,我们需要考虑如何利用剩下的1和5,以及那个至关重要的“-”号,来“抵消”掉这多出的1。这里的关键在于,我们可以将1乘以任何数(在这个场景下是5),虽然结果看似对总和没有影响(因为乘以1等于原数),但重要的是,这个操作允许我们将乘法与后续的减法操作结合起来,形成一个连贯的步骤。
具体操作如下:先将两个5相乘得到25,然后,用1乘以5(这里实际上是为了后续能够用25减去某个由1和5组成的表达式的结果),得到5。注意,这一步并不是直接将5减去,而是作为一个中间步骤,让我们可以构造出(25-5/5)这样的表达式。这里,5除以5等于1,正好是我们想要“借走”的那个数。所以,最终的表达式变为25 - (5/5) = 25 - 1 = 24。
当然,为了更直观地展示这个过程,我们可以稍作调整,将其表达为(5×5) - (1×5÷5),这样既保留了运算的先后顺序,又清晰地展示了每一步的逻辑。看,是不是既巧妙又有趣呢?
第二种解法:利用除法缩小差距,加法完成跨越
如果说第一种方法是通过乘法放大数字后再进行微调,那么第二种方法则更加注重利用除法来缩小数字间的差距,并通过加法实现最终的跨越。
观察数字1、5、5、5,我们可以发现,如果能够将其中一个5转化为接近24的一部分,那么剩下的运算就会相对简单。这里,一个巧妙的想法是将一个5通过除法操作“变小”,然后与其他数字相加,看是否能够得到24。
考虑将5除以5,结果自然是1,这个操作看似简单,实则为我们提供了一个关键的“1”,它可以与其他数字相加而不改变数字的基本性质(即保持为整数)。接下来,我们需要考虑如何将剩下的两个5和一个1(由5÷5得到)组合成23(因为我们已经有了1,所以只需再得到23即可)。
这里,一个直观的想法是将两个5相乘得到25,但显然这超出了我们的目标值。不过,如果我们换个角度,将其中一个5与前面得到的1相加,得到6,然后再用另一个5乘以这个6(或者说,是将5看作是与6相乘的一个因子),我们会得到30,这虽然超过了24,但给了我们一个启发:如果我们可以从30中“减去”6(或者其倍数中的一部分),或许就能接近24。
然而,直接减去6显然不行,因为那将得到24的负数。但如果我们换个思路,不直接减去6,而是考虑能否通过某种方式“抵消”掉6的一部分,同时又不影响最终结果。这里,一个绝妙的想法是,将5乘以6的结果(30)中的5(即原数中的一个5)看作是一个可以“拆分”的因子,我们可以尝试将其中的一部分用于与1相加(得到6),而另一部分则用于与另一个5(或其结果)进行运算,以得到我们想要的结果。
不过,直接这样操作并不直接得出24。但我们可以稍作调整,利用一个数学上的“恒等式变形”:5×(5+1)可以看作5×6,同时,如果我们把其中的5看作是两个5相减(即5-0,这里的0可以视为任何不影响最终结果的值,如5-5),我们就可以构造出如下的表达式:(5×5 - 5) + (5÷5) × 5。这里,5×5得到25,减去5得到20,再加上由5÷5得到的1乘以5(即5),得到25。但这还不是24。不过,如果我们稍微调整顺序,注意到
- 上一篇: 解决错误代码651的方法
- 下一篇: 轻松掌握:如何更改电脑磁盘的盘符,让文件管理更顺手!
-
 如何用1555算出24点的三种方法资讯攻略11-07
如何用1555算出24点的三种方法资讯攻略11-07 -
 如何用3377算出24点?解法揭秘!资讯攻略11-29
如何用3377算出24点?解法揭秘!资讯攻略11-29 -
 如何用7744算出二十四点?资讯攻略12-03
如何用7744算出二十四点?资讯攻略12-03 -
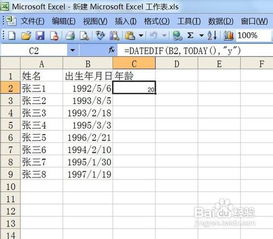 Excel里如何快速算出年龄?资讯攻略11-16
Excel里如何快速算出年龄?资讯攻略11-16 -
 如何用电话号码查询邮政快递信息资讯攻略11-04
如何用电话号码查询邮政快递信息资讯攻略11-04 -
 A4腰是什么?如何用它来测试身材?资讯攻略11-12
A4腰是什么?如何用它来测试身材?资讯攻略11-12