揭秘:互质数究竟是什么?
互质数,作为数学中的一个基本概念,涉及到整数之间的特定关系。本文旨在简明扼要地介绍互质数的含义、性质、判别方法以及实际应用,同时注重关键词布局和密度,确保内容的原创性和结构的清晰性,以优化用户阅读体验和搜索引擎友好度。
互质数,英文名称为relatively prime,指的是两个或多个整数的公因数只有1的非零自然数。简而言之,如果两个数的最大公约数为1,则这两个数互质。互质数的概念在数论中占有重要地位,它不仅是理解其他数学概念的基础,还在实际问题的解决中发挥关键作用。
互质数的定义
互质数的定义可以从以下几个方面进行阐述:
1. 基本定义:两个非零自然数,如果它们的公因数只有1,则这两个数互质。例如,2和3互质,因为它们的唯一公因数是1。
2. 多个数的互质:对于多个非零自然数,如果它们两两之间的最大公因数都是1,则这些数互质。例如,2、3、5互质,因为这三者之间任意两个数的最大公因数都是1。
3. 特殊情况:
任意两个不同的质数互质,如2和3。
1和任何自然数互质,如1和7。
一个质数与一个非其倍数的合数互质,如3和10。
互质数的性质
互质数具有以下几个重要性质:
1. 最大公约数与最小公倍数:几个两两互质的数,它们的最大公约数是1,最小公倍数是它们的乘积。这一性质在解决某些数学问题时非常有用。
2. 整除性质:两个数分别除以它们的最大公约数,所得的商一定互质。这一性质揭示了互质数与整除之间的关系。
3. 互质数的乘积:互质的两个数相乘,所得的数不一定是合数。例如,1与17互质,1×17=17,而17是质数。
4. 表示范围:两个互质的数a和b可以表示(a-1)×(b-1)之后的所有数字,它们最小不能表示的数就是(a-1)×(b-1)-1。
互质数的判别方法
判断两个或多个数是否互质,可以通过以下几种方法:
1. 概念判断法:直接根据互质数的定义判断。如果两个数的公因数只有1,则这两个数互质。
2. 规律判断法:
两个不相同的质数一定是互质数,如7和11。
相邻的两个自然数一定是互质数,如15和16。
相邻的两个奇数一定是互质数,如49和51。
一个质数与一个非其倍数的合数一定是互质数,如3和10。
两个数中的较大数是质数,这两个数一定是互质数,如3和19。
两个数中的较小数是质数,且较大数不是较小数的倍数,这两个数一定是互质数,如7和16。
3. 分解判断法:将两个数进行质因数分解,如果它们的质因数集合没有交集(除了1),则这两个数互质。例如,8=2×2×2,15=3×5,8和15互质。
4. 求差判断法:计算两个数的差,如果差与其中较小数互质,则这两个数互质。例如,194和201,201-194=7,7和194互质,所以194和201互质。
5. 求商判断法:用大数除以小数,如果除得的余数与其中较小数互质,则这两个数互质。例如,317和52,317÷52=6余5,5与52互质,所以317和52互质。
互质数的实际应用
互质数在实际问题中有广泛的应用,特别是在解决最大公约数、最小公倍数、铺地砖、相遇问题等方面:
1. 最大公约数与最小公倍数:在求两个数的最大公约数和最小公倍数时,如果这两个数互质,则它们的最大公约数为1,最小公倍数为它们的乘积。
2. 铺地砖问题:例如,用一批正方形地砖铺满一块长24米、宽17米的空地。由于24和17互质,它们的最大公约数为1,所以正方形地砖的最大边长应为1
- 上一篇: 揭秘:轻松查找苹果手机激活时间的神秘路径
- 下一篇: 天津摇号结果如何查询?
-
 揭秘“lost.dir”文件夹:它究竟是做什么的?资讯攻略12-04
揭秘“lost.dir”文件夹:它究竟是做什么的?资讯攻略12-04 -
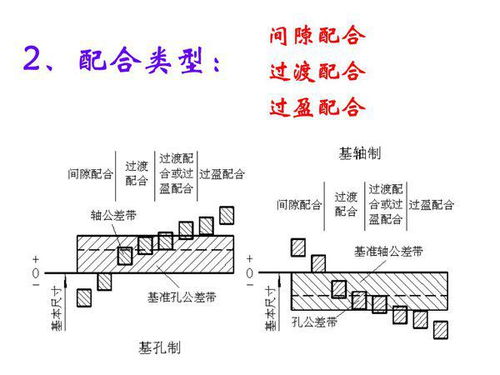 揭秘:过渡配合究竟是什么?资讯攻略12-06
揭秘:过渡配合究竟是什么?资讯攻略12-06 -
 揭秘:盛大白金帐号究竟是什么?资讯攻略03-16
揭秘:盛大白金帐号究竟是什么?资讯攻略03-16 -
 揭秘:磨课究竟是什么?资讯攻略11-13
揭秘:磨课究竟是什么?资讯攻略11-13 -
 揭秘:am:pm究竟是什么品牌?资讯攻略03-07
揭秘:am:pm究竟是什么品牌?资讯攻略03-07 -
 揭秘:三观究竟是什么?详细解析人生三观!资讯攻略02-09
揭秘:三观究竟是什么?详细解析人生三观!资讯攻略02-09












