如何绘制哈夫曼树?
如何绘出神奇的哈夫曼树?一文带你掌握!

在数据结构与算法的奇妙世界里,哈夫曼树(Huffman Tree)无疑是一颗璀璨的明珠。它以其独特的构造方式和广泛的应用领域,吸引了无数编程爱好者的目光。那么,你是否也对这颗神奇的树心生向往呢?别担心,本文将带你一步步揭开哈夫曼树的神秘面纱,让你轻松掌握其绘制方法。
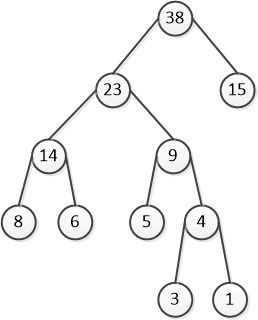
一、哈夫曼树的简介
哈夫曼树,又称最优二叉树,是一种带权路径长度最短的二叉树。这里的“权”可以理解为某个字符在文本中出现的频率或其他重要性指标,“路径长度”则是指从根节点到某个叶子节点的边数之和。哈夫曼树在数据压缩、文件编码等领域有着广泛的应用,特别是在霍夫曼编码中,它能够帮助我们实现高效的数据压缩。

二、绘制哈夫曼树的步骤
1. 准备字符及其权值
首先,我们需要准备一组字符及其对应的权值。这些权值通常代表了字符在文本中出现的频率。例如,我们有一组字符及其权值如下:
A: 5
B: 9
C: 12
D: 13
E: 16
F: 45
2. 构建初始优先队列
接下来,我们将这些字符及其权值放入一个优先队列(通常使用最小堆实现)中。优先队列的作用是按照权值的大小对字符进行排序,以便在后续步骤中能够快速找到权值最小的两个节点。
3. 合并节点
现在,我们开始进行节点的合并操作。具体步骤如下:
从优先队列中取出权值最小的两个节点,作为新节点的左子节点和右子节点。
新节点的权值等于这两个子节点权值之和。
将新节点插入到优先队列中。
重复上述步骤,直到优先队列中只剩下一个节点为止。这个节点就是哈夫曼树的根节点。
4. 构建哈夫曼树
在合并节点的过程中,我们可以同时构建哈夫曼树的结构。具体来说,每次合并两个节点时,都会创建一个新的父节点,并将这两个节点作为其子节点。这样,随着合并操作的进行,哈夫曼树的结构也会逐渐完善。
5. 绘制哈夫曼树
最后一步就是绘制哈夫曼树了。根据前面构建的树结构,我们可以使用图形化工具或编程语言来绘制出哈夫曼树的图形表示。在绘制时,需要注意节点的排列和边的连接,以确保树的结构清晰明了。
三、示例详解
为了让你更好地理解哈夫曼树的绘制过程,下面我们以一组具体的字符及其权值为例进行详细讲解。
字符及其权值:
A: 5
B: 9
C: 12
D: 13
E: 16
F: 45
步骤一:构建初始优先队列
我们将这些字符及其权值放入一个最小堆中,得到如下优先队列:
[A(5), B(9), C(12), D(13), E(16), F(45)]
步骤二:合并节点
1. 取出权值最小的两个节点A和B,合并得到新节点AB,权值为14。
优先队列变为:[C(12), D(13), E(16), F(45), AB(14)]
2. 取出权值最小的两个节点C和D,合并得到新节点CD,权值为25。
优先队列变为:[E(16), F(45), AB(14), CD(25)]
3. 取出权值最小的两个节点AB和E,合并得到新节点ABE,权值为30。
优先队列变为:[F(45), CD(25), ABE(30)]
4. 取出权值最小的两个节点CD和ABE,合并得到新节点CDABE,权值为55。
优先队列变为:[F(45), CDABE(55)]
5. 取出权值最小的两个节点F和CDABE,合并得到哈夫曼树的根节点FCDABE,权值为100。
优先队列为空。
步骤三:构建哈夫曼树
在合并节点的过程中,我们可以同时构建出哈夫曼树的结构。具体结构如下:
```
FCDABE(100)
/ \
F(45) CDABE(
- 上一篇: 有效方法:如何彻底消除黑眼圈
- 下一篇: 揭秘约数的奥秘:你所不知的数学小秘密
-
 绘制家族树的创意指南资讯攻略11-15
绘制家族树的创意指南资讯攻略11-15 -
 打造精美简约的知识树绘画指南资讯攻略11-30
打造精美简约的知识树绘画指南资讯攻略11-30 -
 如何让平安树茂盛生长资讯攻略11-30
如何让平安树茂盛生长资讯攻略11-30 -
 如何养护平安树?资讯攻略11-27
如何养护平安树?资讯攻略11-27 -
 如何深入分析进化树资讯攻略12-06
如何深入分析进化树资讯攻略12-06 -
 如何种植平安树及需要注意哪些事项?资讯攻略11-28
如何种植平安树及需要注意哪些事项?资讯攻略11-28












