揭秘:如何精准计算逃逸速度?
逃逸速度怎么计算
逃逸速度是一个在天文学和宇宙航行中至关重要的概念。它指的是一个物体在天体表面上垂直向上发射时,所需要具备的最小速度,以克服该天体的引力并完全逃离其吸引范围。以下将从多个维度探讨逃逸速度的计算方法及其相关因素。
一、逃逸速度的定义
逃逸速度,也称为“脱离速度”或“第二宇宙速度”,是天体表面上物体摆脱该天体万有引力的束缚飞向宇宙空间所需的最小速度。这个概念在航天工程、宇宙探测等领域有着广泛的应用。比如,地球的逃逸速度为11.2公里/秒,也就是说,一个物体在地球表面以11.2公里/秒或更高的速度垂直向上发射,就可以完全逃离地球的引力,进入宇宙空间。

二、逃逸速度的计算公式
逃逸速度的计算主要依赖于天体的质量和半径。一个通用的逃逸速度计算公式为:

V = √(2GM/R)

其中:
V 是逃逸速度。
G 是万有引力常数,约为6.67430×10^-11 m^3 kg^-1 s^-2。
M 是天体的质量。
R 是天体的半径。
例如,以地球为例,其质量约为5.972×10^24千克,半径约为6370千米。将这些数值代入公式,可以计算出地球的逃逸速度:
V = √(2×6.67430×10^-11×5.972×10^24/6370×10^3) ≈ 11.17 公里/秒
三、逃逸速度与质量的关系
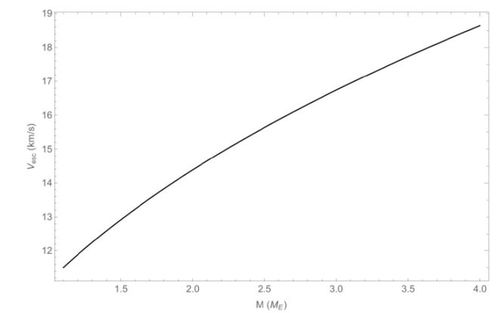
逃逸速度直接依赖于天体的质量。天体质量越大,其引力就越强,因此需要的逃逸速度也越大。反之,一个较轻的天体将会有较小的逃逸速度。这一点可以从逃逸速度的计算公式中看出,逃逸速度V与天体质量M的平方根成正比。
四、逃逸速度与半径的关系
除了质量,逃逸速度还依赖于天体的半径。半径较小的天体,其逃逸速度通常较大。这可以从逃逸速度的计算公式中看出,逃逸速度V与天体半径R的平方根成反比。这意味着,对于两个质量相同的天体,半径较小的那个会有更大的逃逸速度。
五、逃逸速度与大气层、自转速度等因素的关系
虽然逃逸速度主要取决于天体的质量和半径,但在实际应用中,还需要考虑其他因素,如大气层、自转速度等。
大气层:天体的大气层可以对逃逸速度产生一定影响。例如,地球的大气层在物体上升过程中会产生阻力,这会使得实际需要的逃逸速度略高于理论计算值。
自转速度:天体的自转也会影响逃逸速度。如果发射方向与天体自转方向一致,所需的逃逸速度可能会稍微降低;反之,如果方向相反,所需的逃逸速度则会增加。
六、逃逸速度与不同天体的比较
不同天体的逃逸速度存在显著差异。以下是几个典型天体的逃逸速度:
地球:逃逸速度为11.2公里/秒。
太阳:逃逸速度约为每秒一百英里(约合160.9公里/秒)。
黑洞:黑洞的逃逸速度极大,理论上可以达到光速(30万千米/秒)。如果一个天体的逃逸速度达到了光速,那么该天体就被认为是黑洞。
七、逃逸速度在航天工程中的应用
逃逸速度在航天工程中有着广泛的应用。例如,在发射宇宙探测器或载人飞船时,需要确保飞船的速度达到或超过目标天体的逃逸速度,以确保飞船能够成功逃离天体的引力束缚,进入宇宙空间。
此外,逃逸速度还用于计算天体之间的引力势能和动能关系。通过计算逃逸速度,可以了解天体之间的引力相互作用,这对于研究天体运动规律、宇宙结构等方面具有重要意义。
八、逃逸速度与第一宇宙速度、第三宇宙速度的比较
第一宇宙速度:也称为环绕速度或低地球轨道速度,是物体绕地球做圆周运动所需的最小速度。第一宇宙速度约为7.9公里/秒。
逃逸速度:即第二宇宙速度,是物体逃离地球引力束缚所需的最小速度。逃逸速度约为11.2公里/秒。
第三宇宙速度:也称为太阳逃逸速度或星际飞行速度,是物体从地球表面发射后能够飞出太阳系所需的最小速度。第三宇宙速度约为16.7公里/秒(选择航天器入轨速度与地球公转速度方向一致时)。
可以看出,逃逸速度(第二宇宙速度)恰好等于第一宇宙速度的根号2倍。而第三宇宙速度则需要在逃逸速度的基础上再加上额外的速度,以确保物体能够飞出太阳系。
九、逃逸速度的数学推导
逃逸速度的计算可以通过
- 上一篇: 天猫魔盒观看电视直播教程
- 下一篇: 轻松指南:如何高效报销新农合
-
 揭秘:如何精准计算存货周转期?资讯攻略11-24
揭秘:如何精准计算存货周转期?资讯攻略11-24 -
 逃逸塔分离后的神秘归宿资讯攻略03-01
逃逸塔分离后的神秘归宿资讯攻略03-01 -
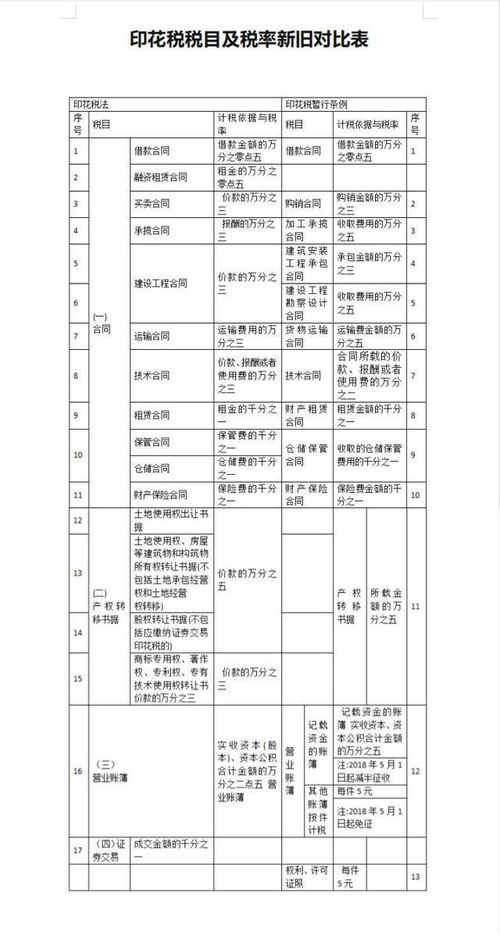 揭秘:如何精准计算适用税率?资讯攻略11-25
揭秘:如何精准计算适用税率?资讯攻略11-25 -
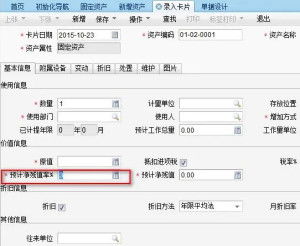 揭秘:如何精准计算预计净残值?资讯攻略11-29
揭秘:如何精准计算预计净残值?资讯攻略11-29 -
 揭秘:如何精准计算负债率?资讯攻略10-31
揭秘:如何精准计算负债率?资讯攻略10-31 -
 揭秘:精神损失费如何精准计算?资讯攻略11-25
揭秘:精神损失费如何精准计算?资讯攻略11-25