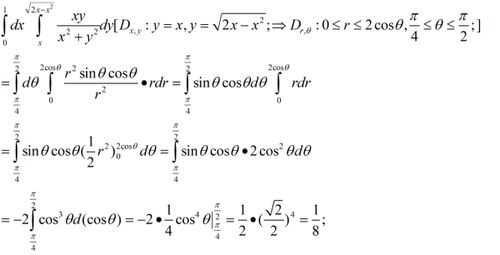一维热传导公式是什么？

在日常生活中，无论是触摸一杯刚泡好的热茶，还是感受到冬日里从暖气片中散发出的温暖，都离不开热传导这一物理现象。热传导是热量从高温物体传递到低温物体的过程，它无处不在，影响着我们的生活。在一维热传导中，热量在一条直线或一维方向上传递，这种传递方式可以用一个简单的数学公式来描述，那就是一维热传导公式。本文将详细介绍一维热传导公式的各个方面，包括它的定义、推导、应用以及实际意义，让读者能够轻松理解这一重要的物理概念。

一维热传导公式的定义

一维热传导公式是描述热量在一维方向上传递速率与温度梯度之间关系的数学表达式。它的基本形式为：

\[q = -kA\frac{\Delta T}{\Delta x}\]

其中，\(q\)表示单位时间内通过某一截面的热量（也称为热流密度），单位是\(W/m^2\)（瓦特每平方米）；\(k\)是材料的热导率，单位是\(W/(m \cdot K)\)（瓦特每米每开尔文），表示材料传递热量的能力；\(A\)是热量传递的截面积，单位是\(m^2\)（平方米）；\(\Delta T\)是温度差，单位是\(K\)（开尔文）或\(°C\)（摄氏度），表示热量传递方向两端的温度差异；\(\Delta x\)是热量传递方向上的距离，单位是\(m\)（米），表示热量传递所经过的路径长度。

这个公式中的负号（-）意味着热量传递的方向是从高温区向低温区，即热量传递方向与温度梯度方向相反。

一维热传导公式的推导

一维热传导公式的推导基于傅立叶热传导定律，该定律是热传导现象的基本规律之一。傅立叶定律指出，热流密度\(q\)与温度梯度成正比，且方向与温度梯度方向相反。

在一维情况下，温度梯度可以表示为\(\frac{\Delta T}{\Delta x}\)，即温度差\(\Delta T\)与距离\(\Delta x\)的比值。因此，根据傅立叶定律，我们有：

\[q = -k\frac{\Delta T}{\Delta x}\]

然而，在实际应用中，热量传递往往发生在具有一定截面积的物体中，如一根金属棒或一根管道。为了计算整个截面的热量传递速率，我们需要将热流密度\(q\)乘以截面积\(A\)，于是得到一维热传导公式的完整形式：

\[q = -kA\frac{\Delta T}{\Delta x}\]

一维热传导公式的应用

一维热传导公式在工程、物理、化学等多个领域都有广泛的应用。下面，我们通过几个具体的例子来展示其应用。

例1：金属棒的加热

假设我们有一根长度为\(L\)的金属棒，其一端温度为\(T_1\)，另一端温度为\(T_2\)，且\(T_1 > T_2\)。金属棒的热导率为\(k\)，截面积为\(A\)。我们想要知道单位时间内通过金属棒某一截面的热量。

根据一维热传导公式，我们有：

\[q = -kA\frac{T_1 - T_2}{L}\]

这个公式告诉我们，单位时间内通过金属棒某一截面的热量与温度差成正比，与金属棒的长度成反比，与热导率和截面积成正比。

例2：房屋的保温

在建筑行业，保温材料的性能对房屋的节能效果至关重要。假设我们有两种保温材料，它们的热导率分别为\(k_1\)和\(k_2\)，且\(k_1 < k_2\)，即第一种材料的保温性能更好。现在，我们需要决定使用哪种材料来建造房屋的保温层。

根据一维热传导公式，我们知道，在相同的温度差和厚度下，热导率更低的材料传递的热量更少，因此保温效果更好。因此，在这个例子中，我们应该选择第一种材料来建造房屋的保温层。

例3：热管的散热

热管是一种高效的散热元件，广泛应用于电子设备、汽车和航空航天等领域。热管的工作原理是利用工作介质在蒸发段吸热汽化，然后在冷凝段放热液化，从而实现热量的传递。

在热管的一维热传导分析中，我们可以将热管看作一根具有特定热导率的金属棒。通过一维热传导公式，我们可以计算出热管在不同温度差和长度下的散热能力，从而优化设计热管的尺寸和材料。

一维热传导公式的实际意义

一维热传导公式不仅是一个数学表达式，它还具有深刻的实际意义。它揭示了热量传递的基本规律，即热量总是从高温区向低温区传递，且传递速率与温度差成正比，与传递路径的长度成反比。这一规律对于理解各种热传导现象、设计高效的热传导材料和设备具有重要意义。

此外，一维热传导公式还为许多工程问题提供了解决方案。例如，在能源工程中，我们可以通过优化热传导路径和材料来提高热效率；在材料工程中，我们可以利用一维热传导公式来评估材料的保温性能；在环境工程中，我们可以通过控制温度差来减少热量损失和环境污染。

结论

一维热传导公式是描述热量在一维方向上传递速率与温度梯度之间关系的数学表达式。它基于傅立叶热传导定律，具有广泛的应用和深刻的实际意义。通过理解一维热传导公式的定义、推导、应用以及实际意义，我们可以更好地掌握热传导现象的基本规律，为解决各种工程问题提供有力的工具和方法。同时，这也为我们进一步优化热传导材料和设备、提高能源利用效率、减少环境污染提供了可能。因此，学习和掌握一维热传导公式对于我们理解和应用热传导现象具有重要意义。