三次方公式具体是什么？

三次方公式，听起来可能有些抽象，但其实它与我们日常生活和学习中的许多内容息息相关。无论是在数学、物理学、经济学，还是在其他各种科学领域，三次方公式都扮演着重要的角色。那么，三次方公式究竟是什么呢？接下来，我们就来详细探讨一下这个有趣而实用的概念。

三次方公式的定义

首先，让我们从最基本的定义开始。三次方公式，简单来说，就是关于一个变量的三次幂的数学表达式。它的一般形式可以表示为：ax³ + bx² + cx + d，其中a、b、c和d是常数，x是变量。这个公式其实是一种多项式，可以用来表示和计算许多复杂的函数和关系。

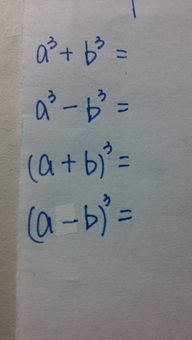
然而，当我们提到“三次方”时，通常更直接地是指一个数的立方运算，即这个数乘以它自己两次。用数学符号表示就是：a³ = a × a × a。这里，a是任意实数，而a³则表示a的三次方，也就是a的立方。

三次方的计算

计算一个数的三次方其实非常简单。你只需要将这个数乘以它自己两次就可以了。例如，要计算3的三次方，我们只需要做这样的计算：3³ = 3 × 3 × 3 = 27。同样地，要计算2的三次方，我们只需要计算2 × 2 × 2 = 8。

除了直接计算，我们还可以使用指数表达式来表示三次方的运算。例如，a³可以写成a × a²，也就是先将a乘以自己得到a²，然后再乘以a。这种表示方法在数学中非常常见，也很方便。

三次方公式的应用

三次方公式不仅仅是一个简单的数学表达式，它在许多领域都有着广泛的应用。

1. 数学

在数学中，三次方公式经常用于解决多元函数的问题和求解方程式的解。例如，在解一元三次方程时，我们就需要用到三次方公式和相关的代数技巧来找到方程的解。此外，三次方公式还可以用于复杂的图形计算，比如计算不同形状的体积和表面积。

2. 物理学

在物理学中，三次方公式同样有着重要的作用。它经常用于计算物理学中的各种复杂运动，比如抛物运动、弹道运动等。在这些运动中，物体的位置和速度等参数往往与时间的三次方有关。此外，在力学中，三次方公式还可以用于计算不同受力和受力状态下的物体行为。

3. 经济学

在经济学中，三次方公式也发挥着重要的作用。例如，它可以用于计算投资回报率、投资风险等经济指标。这些指标对于投资者和企业来说非常重要，因为它们可以帮助他们做出更明智的决策。

三次方的性质和特点

除了了解三次方公式的定义和应用外，我们还可以进一步探讨三次方的一些性质和特点。

1. 立方根

如果一个数的立方等于a，那么这个数就叫做a的立方根或三次方根。例如，因为2³ = 8，所以2就是8的立方根。同样地，因为(-2)³ = -8，所以-2就是-8的立方根。

2. 立方根的性质

正数的立方根是正数，负数的立方根是负数，0的立方根是0。

在实数范围内，任何实数的立方根只有一个。

在实数范围内，负数不能开平方，但可以开立方。

立方与开立方运算互为逆运算。

3. 复数范围内的立方根

在复数范围内，情况就变得更加有趣了。任何非0的数都有且仅有3个立方根，其中一个是实根，另外两个是共轭虚根。这三个立方根均匀分布在以原点为圆心、算术根为半径的圆周上，它们对应的点构成正三角形。这个性质在复数理论和相关应用中非常重要。

三次方公式的推广和变形

除了基本的三次方公式ax³ + bx² + cx + d外，我们还可以根据需要进行推广和变形。例如，在数学中，我们经常使用到“三数和立方公式”。这个公式涉及到三个数的立方和与它们两两相乘的平方和以及三者的乘积的组合，具体形式为：a³ + b³ + c³ + 3a²b + 3ab² + 3a²c + 3ac² + 3b²c + 3bc² + 6abc。这个公式在某些特定的情况下会被使用，尤其是在解决多项式方程或进行代数计算时。

三次方公式的实际应用案例

为了更好地理解三次方公式的应用，我们可以来看一些具体的案例。

案例一：计算物体的体积

假设我们有一个边长为a的正方体，那么它的体积就是a³。这是因为正方体的体积等于其边长的三次方。通过这个简单的例子，我们可以直观地理解三次方公式在几何计算中的应用。