轻松掌握!如何进行因式分解?
在数学学习中,因式分解是一项至关重要的技能。它不仅能够帮助我们简化复杂的数学表达式,还能在解决方程、不等式等问题时发挥重要作用。那么,怎么进行因式分解呢?本文将详细介绍因式分解的基本概念、方法以及几个常见的例子,帮助你掌握这一技能。
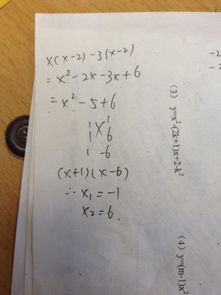
首先,我们需要明确什么是因式分解。因式分解,简而言之,就是将一个多项式表示为几个整式的乘积。例如,多项式 x^2 - 4 可以分解为 (x + 2)(x - 2)。在这个过程中,我们将一个复杂的多项式转化为了几个简单的整式,从而方便了后续的计算和问题解决。
接下来,我们介绍几种常见的因式分解方法。
第一种方法是提公因式法。如果一个多项式的各项都含有某个相同的因子,那么这个因子就可以提取出来,使得多项式得到简化。例如,对于多项式 3x^2 + 6x,我们可以提取公因子 3x,得到 3x(x + 2)。这种方法的关键在于识别并提取出多项式中的公因子。
第二种方法是公式法。对于一些特定形式的多项式,我们可以利用已知的公式进行因式分解。例如,平方差公式 a^2 - b^2 = (a + b)(a - b) 和完全平方公式 a^2 + 2ab + b^2 = (a + b)^2、a^2 - 2ab + b^2 = (a - b)^2 就是两种常见的公式。利用这些公式,我们可以迅速地将一些特定形式的多项式进行因式分解。
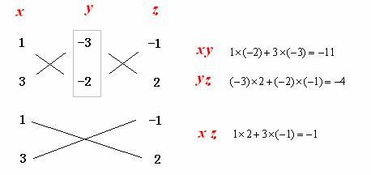
第三种方法是十字相乘法。这种方法主要用于二次多项式的因式分解。具体来说,就是将二次多项式 ax^2 + bx + c 的系数 a、b、c 分别看作是两个因式的一次项系数和常数项的乘积,然后通过交叉相乘并相加的方式,验证是否满足原多项式的中间项系数 b。如果满足,则这两个因式就是原多项式的因式分解结果。例如,对于多项式 x^2 - 5x + 6,我们可以将其看作 (x - ?) 和 (x - ?) 的乘积,然后通过尝试不同的数值,找到满足条件的因式 x - 2 和 x - 3,从而得到因式分解结果 (x - 2)(x - 3)。
除了以上三种方法外,还有一些其他的方法可以用于特定情况下的因式分解。例如,分组分解法就是将多项式分组后,再对每一组进行因式分解;求根法则是通过求解多项式的根来找到其因式;换元法则是通过引入新的变量来简化多项式,从而便于进行因式分解。然而,这些方法的应用范围相对有限,通常在特定情况下才会使用。
现在,我们来看几个具体的例子,以加深对因式分解方法的理解。
例一:分解多项式 2x^3 - 4x^2 - 6x。
首先,我们可以提取公因子 2x,得到 2x(x^2 - 2x - 3)。然后,我们注意到括号内的多项式是一个二次多项式,可以尝试使用十字相乘法进行因式分解。将 -3 分解为 -3 和 1 的乘积,并尝试将它们分别与 x^2 和 -2x 相乘,得到 -3x 和 x。验证后发现,它们的乘积确实满足原多项式的中间项系数 -2x,因此我们可以将原多项式分解为 2x(x - 3)(x + 1)。
例二:分解多项式 x^4 - 16。
这是一个平方差形式的多项式,可以直接应用平方差公式进行因式分解。得到 (x^2 + 4)(x^2 - 4)。然后,我们注意到括号内的后一个多项式也是一个平方差形式的多项式,可以继续应用平方差公式进行因式分解。最终得到 (x^2 + 4)(x + 2)(x - 2)。
例三:分解多项式 x^2 - 5xy + 6y^2。
这是一个二次多项式,可以尝试使用十字相乘法进行因式分解。将 6y^2 分解为 2y 和 3y 的乘积,并尝试将它们分别与 x 和 -5y 相乘,得到 -2xy 和 -3y^2(注意这里的负号)。验证后发现,它们的乘积确实满足原多项式的中间项系数 -5xy(注意负号的处理),因此我们可以将原多项式分解为 (x - 2y)(x - 3y)。
通过以上的介绍和例子,我们可以发现因式分解是一项需要灵活运用多种方法和技巧的技能。在掌握基本方法的基础上,我们还需要通过大量的练习来培养自己的直觉和判断力,以便在遇到复杂多项式时能够迅速找到合适的因式分解方法。
此外,值得注意的是因式分解的结果并不是唯一的。例如,对于多项式 x^2 - 4,我们既可以将其分解为 (x + 2)(x - 2),也可以将其看作 (2 + x)(2 - x) 的相反数(即乘以 -1 后再分解)。因此,在进行因式分解时,我们需要保持灵活性并接受多种可能的结果。
总之,因式分解是数学学习中不可或缺的一项技能。通过掌握基本方法和技巧、进行大量练习以及培养自己的直觉和判断力,我们可以更好地应对各种复杂的多项式并找到它们的因式分解结果。希望本文能够帮助你掌握这一技能并在未来的数学学习中取得更好的成绩。
- 上一篇: 天玑1200性能与哪款骁龙处理器相当?
- 下一篇: 如何查询车辆的年检信息?
-
 掌握技巧:轻松学会因数分解法资讯攻略02-20
掌握技巧:轻松学会因数分解法资讯攻略02-20 -
 十字相乘法如何进行因式分解?资讯攻略02-10
十字相乘法如何进行因式分解?资讯攻略02-10 -
 探秘因数分解:轻松掌握分解技巧资讯攻略12-04
探秘因数分解:轻松掌握分解技巧资讯攻略12-04 -
 如何让幼儿园小朋友更好地理解数字分解?资讯攻略11-08
如何让幼儿园小朋友更好地理解数字分解?资讯攻略11-08 -
 《侠客道》英雄养成秘籍:深度解析英雄分解策略资讯攻略04-09
《侠客道》英雄养成秘籍:深度解析英雄分解策略资讯攻略04-09 -
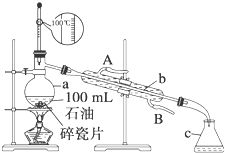 轻松掌握!减压蒸馏提纯有机化合物的实用方法资讯攻略11-01
轻松掌握!减压蒸馏提纯有机化合物的实用方法资讯攻略11-01












