直角三角形斜边长度计算方法

揭秘直角三角形斜边的计算奥秘：从勾股定理到实际应用

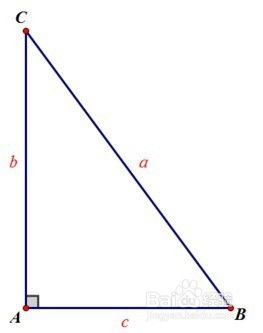
在数学的浩瀚宇宙中，直角三角形犹如一颗璀璨的星辰，不仅因其形状简洁明了，更因它蕴含了众多深刻的数学原理和实际应用。今天，我们就来一起揭开直角三角形斜边计算的神秘面纱，从古老的勾股定理到现代的实际应用，带你领略这一领域的无穷魅力。

直角三角形，简单来说，就是一个有一个90度角的三角形。在这个三角形中，最长的那条边被称为斜边，而与斜边相邻的两条边则分别被称为直角边。对于很多人来说，如何准确计算直角三角形的斜边长度一直是个难题。但幸运的是，我们有一个强大的数学工具——勾股定理，来帮助我们解决这个问题。

勾股定理，这个古老的数学原理，最早可以追溯到公元前11世纪的西周时期。我国数学家商高曾提出“勾三股四弦五”的勾股定理特例，而西方则普遍认为是古希腊数学家毕达哥拉斯最早发现并证明了这一定理。勾股定理的内容简洁明了：在直角三角形中，直角边的平方和等于斜边的平方。用数学公式表示就是：a² + b² = c²，其中a和b是直角边的长度，c是斜边的长度。

这个定理看似简单，但实际上却蕴含着极其深刻的数学意义。它不仅揭示了直角三角形三边之间的数量关系，还为后续的三角函数、解析几何等领域的发展奠定了坚实的基础。更重要的是，勾股定理在现实生活中的应用也极为广泛，从建筑设计到工程测量，从物理学到天文学，几乎无处不在。

那么，如何利用勾股定理来计算直角三角形的斜边长度呢？其实方法非常简单。首先，我们需要知道直角三角形的两个直角边的长度。然后，将这两个长度的平方相加，得到的结果就是斜边长度的平方。最后，对这个结果开平方根，就可以得到斜边的实际长度了。

例如，如果我们有一个直角三角形，其中一条直角边的长度为3厘米，另一条直角边的长度为4厘米。那么，根据勾股定理，我们可以计算出斜边的长度为：c = √(3² + 4²) = √(9 + 16) = √25 = 5厘米。

当然，在实际应用中，我们遇到的直角三角形往往不会这么简单。有时，我们可能只知道直角三角形的一个直角边长度和一个锐角的度数，或者只知道斜边长度和一个锐角的度数。这时，我们就需要借助三角函数来求解了。

三角函数是数学中一类重要的函数，它们描述了直角三角形中边与角之间的关系。其中，正弦（sin）、余弦（cos）和正切（tan）是最常用的三个三角函数。正弦函数的定义为：sinA = 对边/斜边；余弦函数的定义为：cosA = 邻边/斜边；正切函数的定义为：tanA = 对边/邻边。通过这三个函数，我们可以很方便地在直角三角形的边与角之间进行转换和求解。

例如，如果我们知道一个直角三角形的锐角A的度数为30度，以及它的一个直角边（对边）的长度为3厘米，我们就可以利用正弦函数来求解斜边的长度：sin30° = 3/c，其中c为斜边的长度。由于sin30°的值为1/2，所以我们可以得到：1/2 = 3/c，进而解得c = 6厘米。同样地，如果我们知道斜边的长度和一个锐角的度数，也可以利用余弦函数或正切函数来求解另一个直角边的长度。

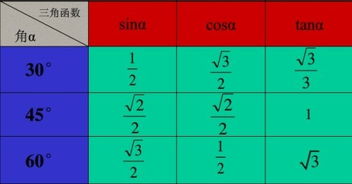
除了三角函数之外，我们还可以利用一些特殊的直角三角形来快速求解斜边的长度。例如，对于30°-60°-90°的直角三角形来说，它的三边之比总是固定的：1:√3:2。其中较短的直角边与斜边的比为1:2，而较长的直角边与斜边的比为√3:2。因此，只要我们知道了这个三角形的一个边的长度，就可以很容易地求出其他两边的长度了。同样地，对于45°-45°-90°的直角三角形来说，它的三边之比也是固定的：1:1:√2。其中两个直角边的长度相等，而斜边的长度是直角边长度的√2倍。

当然，在实际应用中，我们还需要注意一些特殊情况的处理。例如，当直角三角形的两个直角边都是未知数时，我们就需要借助其他条件或方法来求解了。这时，我们可以考虑利用三角形的面积公式、相似三角形的性质或者直角三角形的其他性质来建立方程组进行求解。

总的来说，直角三角形的斜边计算虽然看似简单，但实际上却涉及了众多的数学原理和实际应用。通过勾股定理、三角函数以及特殊直角三角形的性质等方法，我们可以轻松地求解出直角三角形的斜边长度。而这些方法和原理不仅在数学学习中有重要作用，还在建筑、工程、物理、天文等领域发挥着巨大的作用。

在未来的学习和生活中，当我们再次遇到直角三角形时，不妨试着用这些方法和原理去求解它的斜边长度吧！相信在探索的过程中，你会发现更多数学的乐趣和奥秘。同时，也希望你能够将这些知识和方法应用到实际生活中去，用数学的眼光去观察世界、解决问题。因为在这个充满未知和挑战的时代里，数学无疑是我们最强大的武器之一。