直角三角形的斜边求解方法

在几何学中，直角三角形是一个非常基础且重要的形状。它的特点之一是包含一个90度的角，也就是直角。在日常生活中，我们经常会遇到直角三角形，比如建筑物的墙角、楼梯的转角等。在处理直角三角形时，一个常见的问题是：如果已知直角三角形的两条直角边，如何求出斜边的长度呢？这篇文章将详细讲解如何求解直角三角形的斜边，希望能帮助你更好地理解和应用这一几何知识。

一、直角三角形的基本概念

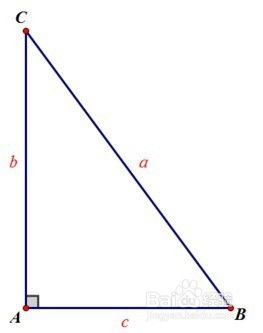
直角三角形是一个包含一个90度角的三角形。这个90度的角通常被称为直角。在直角三角形中，与直角相邻的两条边被称为直角边，而第三条边则被称为斜边。斜边是直角三角形中最长的一条边，也是直角三角形的一个显著特征。

二、勾股定理

求解直角三角形斜边的关键工具是勾股定理。勾股定理是一个古老而重要的数学定理，它描述了在直角三角形中，直角边的平方和等于斜边的平方。用数学公式表示就是：

a² + b² = c²

其中，a和b是直角三角形的两条直角边，c是斜边。

三、应用勾股定理求解斜边

1. 已知两条直角边

如果已知直角三角形的两条直角边a和b的长度，那么可以通过勾股定理求出斜边c的长度。具体步骤如下：

首先，计算两条直角边的平方和，即a² + b²。

然后，求出这个和的平方根，即√(a² + b²)。

这个平方根就是斜边c的长度。

例如，如果一个直角三角形的两条直角边分别是3米和4米，那么斜边的长度可以通过以下步骤计算：

计算3² + 4² = 9 + 16 = 25。

然后，求出25的平方根，即√25 = 5。

因此，斜边的长度是5米。

2. 实际生活中的应用

勾股定理不仅在数学课堂上有用，在现实生活中也有广泛的应用。比如，在建筑和工程领域，工程师们经常需要计算直角三角形的斜边长度来确保结构的稳定性和精确性。在装修时，如果需要在墙上挂一幅画，并且希望画框的顶部与地面的距离恰好等于某个特定的值，那么可以通过勾股定理来计算挂画所需的高度和倾斜角度。

四、特殊情况下的斜边求解

1. 等腰直角三角形

等腰直角三角形是一种特殊的直角三角形，它的两条直角边长度相等。在这种情况下，由于两条直角边相等，我们可以直接通过一条直角边的长度乘以√2来求出斜边的长度。

例如，如果一个等腰直角三角形的直角边长度是4米，那么斜边的长度可以通过以下步骤计算：

由于是等腰直角三角形，所以两条直角边都是4米。

直接计算4 × √2 = 4√2（约等于5.66米）。

因此，斜边的长度是4√2米。

2. 已知斜边和一条直角边

有时，我们可能已知直角三角形的斜边和一条直角边的长度，需要求出另一条直角边的长度。虽然这个问题不是直接求斜边，但它是勾股定理的逆应用，也值得提一下。

例如，如果一个直角三角形的斜边长度是5米，一条直角边长度是3米，那么另一条直角边的长度可以通过以下步骤计算：

首先，根据勾股定理，我们有3² + b² = 5²。

然后，解这个方程求出b，即b² = 5² - 3² = 25 - 9 = 16。

最后，求出b的平方根，即b = √16 = 4。

因此，另一条直角边的长度是4米。

五、勾股定理的证明

虽然这篇文章的重点是讲解如何应用勾股定理求解直角三角形的斜边，但了解勾股定理的证明过程也有助于加深理解。勾股定理的证明有多种方法，其中一种常见的方法是使用面积法。

1. 面积法证明

考虑一个直角三角形，它的两条直角边分别是a和b，斜边是c。我们可以构造两个正方形，一个以a为边长，一个以b为边长，然后将它们拼在一起形成一个大的矩形。这个矩形的长是a+b，宽是a（或b，因为两个正方形是相等的）。同时，我们也可以构造一个以c为边长的正方形。

现在，我们注意到这个大矩形的面积等于两个小正方形的面积之和，即a² + b²。同时，这个大矩形的面积也等于以c为边长的正方形的面积，即c²。因此，我们得出a² + b² = c²，这就是勾股定理。

六、总结

直角三角形是几何学中的一个基础而重要的形状。通过勾股定理，我们可以方便地求解直角三角形的斜边长度。无论是已知两条直角边还是已知斜边和一条直角边，都可以利用勾股定理进行求解。此外，了解勾股定理的证明过程也有助于我们更好地理解和应用这一数学定理。

在日常生活中，勾股定理的应用非常广泛，从建筑和工程到装修和日常生活，都离不开它。因此，掌握勾股定理及其求解方法是非常重要的。希望这篇文章能够帮助你更好地理解直角三角形和勾股定理，并在实际应用中灵活运用它们。