长方体展开图有几种常见的形式？

探索长方体的奇妙世界：揭秘其展开图的多样形态

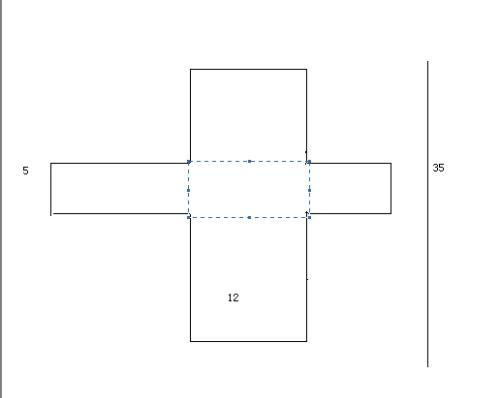
在几何学的浩瀚宇宙中，长方体如同一座规则的立方体城堡，静静地伫立在那里，用它那六个矩形的面诉说着关于空间与结构的故事。然而，当我们尝试将这座城堡“拆解”开来，把它的各个面铺展在平面上时，一个充满趣味和挑战的新世界便悄然展开——这便是长方体的展开图。今天，就让我们一起踏上这场奇妙的探索之旅，去揭开长方体展开图的神秘面纱，看看这个看似简单的几何体究竟能变幻出多少种不同的展开形态。

一、长方体的基本构造与展开图的初识

首先，让我们回顾一下长方体的基本构造。一个长方体由三组平行的、大小相等的矩形面组成，每组面相互垂直。这三个维度上的矩形面，我们可以称之为“长×宽”、“长×高”和“宽×高”。正是这些矩形的不同组合和排列方式，构成了长方体展开图的多样性。

展开图，顾名思义，就是将长方体的各个面展开到同一个平面上，同时保持各面之间的相对位置关系不变。这个过程就像是把一个三维的立体图形“压扁”成一个二维的平面图形。通过展开图，我们可以更加直观地理解和分析长方体的表面结构，甚至可以利用它来制作纸模、包装纸等实际应用。

二、揭开长方体展开图的神秘面纱

那么，长方体的展开图到底有多少种呢？这个问题听起来简单，但实际上却蕴含着深刻的数学原理和组合逻辑。为了找到答案，我们需要对长方体的各个面进行排列组合，同时考虑它们之间的相对位置关系。

1. 基本类型的划分

长方体的展开图可以根据其排列组合方式的不同，大致划分为以下几种基本类型：

“1-4-1”型：即一个较大的矩形面（长×宽或长×高或宽×高）在中间，四周围绕着四个较小的矩形面（两个长×高、两个宽×高或两个长×宽）。这种类型比较常见，因为它保持了长方体两组对面之间的相对位置关系。

“2-3-1”型：由两个较大的矩形面（一组对面）和两个较小的矩形面（另一组对面中的一个）以及一个单独的矩形面（另一组对面中的另一个）组成，呈“田”字形排列。这种类型相对少见，但同样能完整地表示长方体的表面结构。

“2-2-2”型：由三组对面各自的两个矩形面组成，每两个矩形面并排排列，形成三条平行的“跑道”。这种类型在展开图中较为特殊，因为它打破了传统的“面对面”排列方式。

“3-3”型：这种类型相对更为罕见，它要求长方体的三个维度（长、宽、高）中的两个必须相等或接近，才能形成两个较大的矩形面（一组对面）和三个较小的矩形面（另一组对面的三个部分）的排列方式。

2. 具体形态的多样性

在上述基本类型的基础上，长方体的展开图还因为各矩形面大小比例的不同而呈现出更多的具体形态。例如，在“1-4-1”型中，如果长方体的长、宽、高比例差异较大，那么展开图就会呈现出明显的“大包围小”的形态；而如果三个维度接近相等，那么展开图就会显得更加均衡和对称。

同样地，在“2-3-1”型和“2-2-2”型中，不同矩形面之间的比例关系也会影响到展开图的整体形态和视觉效果。有的展开图可能显得紧凑而有序，有的则可能显得松散而凌乱。

3. 组合逻辑的复杂性

除了基本类型和具体形态之外，长方体展开图的多样性还体现在其组合逻辑的复杂性上。由于长方体的每个面都可以作为展开图的起点或终点，而且各面之间的相对位置关系也可以有多种变化，因此即使对于同一个长方体来说，其展开图也可能存在多种不同的排列方式。

这种组合逻辑的复杂性使得长方体展开图的研究成为了一个充满挑战和趣味的数学课题。数学家们通过排列组合、图论等数学工具来分析和探索长方体展开图的规律和特性，为我们揭示了这个看似简单几何体背后隐藏的奥秘。

三、长方体展开图的实际应用与意义

长方体展开图不仅具有数学上的研究价值，还广泛应用于我们的日常生活中。例如，在包装设计中，设计师需要根据产品的形状和大小来选择合适的包装材料，并通过绘制长方体的展开图来确定包装纸的大小和裁剪方式。

在建筑设计中，建筑师也需要利用长方体展开图来分析和优化建筑物的表面结构，以提高其稳定性和美观性。此外，在折纸艺术、纸模制作等领域中，长方体展开图更是不可或缺的工具之一。

除了实际应用之外，长方体展开图的研究还有助于培养我们的空间想象力和逻辑思维能力。通过观察和分析不同形态的展开图，我们可以更加深入地理解长方体的表面结构和空间关系，从而提高我们的几何直觉和数学素养。

四、结语

在这场关于长方体展开图的探索之旅中，我们不仅领略了其多样性和复杂性，更深刻感受到了数学与生活的紧密联系。长方体展开图就像是一扇通往数学世界的窗口，让我们在欣赏其美丽形态的同时，也领略到了数学的魅力和力量。

未来，随着数学研究的不断深入和科技的不断发展，相信长方体展开图将会为我们带来更多的惊喜和发现。让我们一起期待这个充满无限可能的数学世界吧！