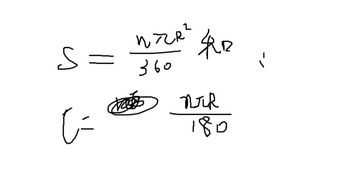长方体周长怎么计算?
长方体作为一种常见的三维几何形状,在日常生活中有着广泛的应用。无论是在建筑设计、工程制造,还是在数学学习中,掌握长方体的基本性质和相关计算公式都是非常重要的。其中,关于长方体周长的问题,虽然在数学上通常讨论的是表面积而非周长,但我们可以从长方体的边和面的角度出发,探讨与其相关的“周长”概念。

首先,需要明确的是,长方体没有直接对应的“周长”概念,因为周长是二维图形(如长方形、正方形、圆形等)的属性,它指的是围绕图形边缘的总长度。长方体作为一个三维立体图形,其边界由六个矩形面组成,而非一条闭合的曲线。然而,如果我们想将长方体的某个维度与二维图形的周长联系起来,可以分别考虑长方体的各个矩形面的周长。

长方体的每个面都是一个矩形,矩形的周长计算公式是:周长 = 2 × (长 + 宽)。因此,对于长方体来说,如果我们想计算某个特定面的周长,只需将那个面的长和宽代入公式即可。例如,如果长方体的一个面的长为a,宽为b,那么这个面的周长就是2(a + b)。

进一步地,如果我们想计算长方体所有面的“周长总和”(尽管这不是一个标准的数学概念,但可以作为一种类比来理解),我们可以将每个面的周长加起来。长方体有六个面,每个面都有一个与之相对的相同面,因此我们可以计算三个不同面的周长,然后将它们各自乘以2来得到总和。
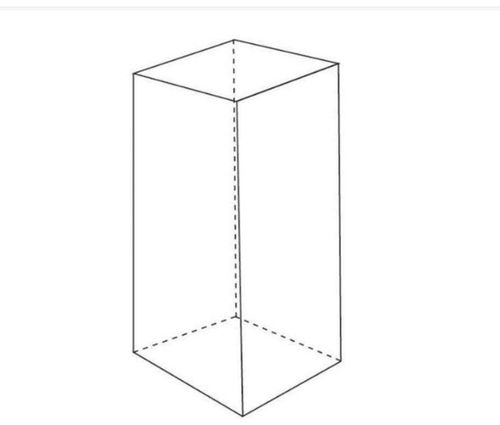
设长方体的三个边长分别为a、b和c,则:
前后两个面的周长总和为:2 × 2(a + b) = 4(a + b)(因为前后两个面的长和宽分别为a和b)。
左右两个面的周长总和为:2 × 2(b + c) = 4(b + c)(因为左右两个面的长和宽分别为b和c)。
上下两个面的周长总和为:2 × 2(a + c) = 4(a + c)(因为上下两个面的长和宽分别为a和c)。
将这三个总和相加,我们得到长方体所有面的“周长总和”为:4(a + b) + 4(b + c) + 4(a + c)。这个表达式虽然不是一个严格的数学定义,但它有助于我们从二维图形的角度理解长方体的边界特征。
然而,在实际应用中,我们更常讨论的是长方体的表面积,而不是上述的“周长总和”。长方体的表面积计算公式是:表面积 = 2(ab + bc + ac)。这个公式考虑了长方体的所有六个面,每个面的面积为长乘以宽,然后将所有面的面积相加得到总面积。表面积是衡量一个三维立体图形外部尺寸大小的重要参数。
在探讨长方体的周长或表面积时,我们还需要注意以下几点:
1. 长方体的边长可以是任意正实数,包括小数和分数。因此,在计算周长或表面积时,我们需要确保使用的边长值是准确的。
2. 当长方体的三个边长相等时(即a = b = c),它就变成了一个正方体。此时,正方体的每个面的周长都是4倍的边长,表面积则是6倍的边长的平方。
3. 长方体的周长或表面积的计算在实际应用中具有重要意义。例如,在包装设计中,我们需要知道长方体的表面积来确定需要多少包装材料;在建筑设计中,我们需要考虑长方体的尺寸来确保空间的合理利用。
4. 除了周长和表面积外,长方体还有其他重要的几何属性,如体积、对角线长度等。这些属性在数学和物理问题中都有广泛的应用。
5. 在进行长方体相关计算时,我们需要注意单位的统一。如果边长以不同的单位给出(如厘米和米),我们需要先进行单位换算才能得到正确的结果。
综上所述,虽然长方体没有直接的“周长”概念,但我们可以通过计算其各个面的周长或表面积来了解其边界特征。在实际应用中,我们需要根据具体问题选择合适的计算公式和方法来得到准确的结果。同时,我们还需要注意单位的统一和计算的准确性,以确保结果的可靠性。
此外,长方体作为几何学中的一个重要概念,在数学教育中也扮演着重要的角色。通过学习长方体的周长和表面积等几何属性,学生可以更好地理解三维空间的概念和几何图形的性质。这不仅有助于提高学生的数学素养,还可以培养他们的空间想象能力和解决问题的能力。
因此,无论是在理论学习还是实际应用中,我们都应该充分重视长方体的相关概念和计算方法。通过深入理解和熟练掌握这些知识,我们可以更好地应对各种与长方体相关的数学问题和实际问题。
- 上一篇: DIY头花制作教程
- 下一篇: 如何查询网上通缉令名单?
-
 揭秘长方体周长:轻松掌握计算公式资讯攻略11-13
揭秘长方体周长:轻松掌握计算公式资讯攻略11-13 -
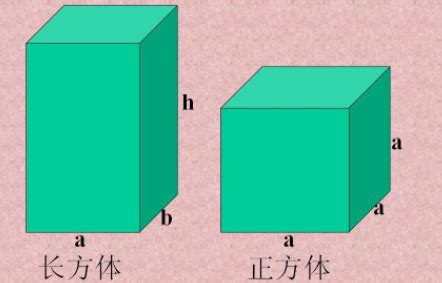 揭秘长方体周长计算的奥秘公式资讯攻略11-14
揭秘长方体周长计算的奥秘公式资讯攻略11-14 -
 正方形周长的计算公式是什么资讯攻略11-01
正方形周长的计算公式是什么资讯攻略11-01 -
 三角形周长计算:使用周长公式的方法资讯攻略11-11
三角形周长计算:使用周长公式的方法资讯攻略11-11 -
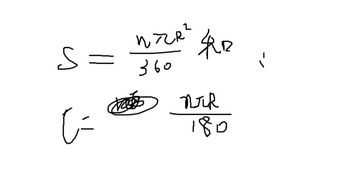 如何计算扇形的周长?资讯攻略11-18
如何计算扇形的周长?资讯攻略11-18 -
 揭秘:轻松掌握圆的周长计算方法资讯攻略11-09
揭秘:轻松掌握圆的周长计算方法资讯攻略11-09