掌握有向图的拓扑排序技巧
有向图的拓扑排序:解锁复杂网络结构的钥匙
在探索计算机科学和数学的浩瀚领域中,有向图(Directed Graph)作为一种强大的工具,广泛应用于各种实际问题的建模与分析中。无论是软件开发中的任务依赖关系,还是电路中的信号流向,有向图都能以其直观而精确的方式描绘出这些复杂系统中的内在联系。而在处理这些有向图时,拓扑排序(Topological Sorting)无疑是一项不可或缺的技术,它为我们提供了一种按照特定顺序遍历图中节点的有效方法。

一、有向图初探
有向图,简而言之,是由节点(或称为顶点)和连接这些节点的有向边组成的图结构。与无向图不同,有向图中的每一条边都带有方向性,它表示从一个节点指向另一个节点的关系。这种方向性使得有向图在描述具有先后次序或依赖关系的系统时尤为得力。

例如,在一个软件开发项目中,我们可以将每个任务视为一个节点,任务之间的依赖关系则用有向边表示。如果任务A必须在任务B之前完成,那么我们就从A向B画一条有向边。这样,整个项目就构成了一个有向图,其中的拓扑结构清晰地揭示了任务之间的执行顺序。
二、拓扑排序的定义与重要性
拓扑排序是一种对有向无环图(Directed Acyclic Graph, DAG)进行线性排序的方法,使得对于每一条有向边(u, v),顶点u在排序中都出现在顶点v之前。这种排序方式保证了图中的每一个节点都能按照其依赖关系被正确地访问。
拓扑排序之所以重要,是因为它在许多实际问题中都有着广泛的应用。在任务调度中,它可以帮助我们确定任务的最佳执行顺序;在编译器设计中,它用于确定编译单元之间的编译顺序;在数据库系统中,它有助于确定表的删除顺序以避免外键约束冲突。此外,拓扑排序还广泛应用于工作流管理、课程安排、路径规划等领域。
三、拓扑排序的实现方法
实现拓扑排序的方法有多种,其中两种最常用的方法是Kahn算法和深度优先搜索(DFS)算法。
1. Kahn算法
Kahn算法是一种基于入度的拓扑排序方法。入度是指向一个节点的边的数量。该算法的基本思想是:不断选择入度为0的节点,将其加入结果列表,并更新其相邻节点的入度。重复这个过程,直到所有节点都被处理完毕或图中存在环。
具体步骤如下:
计算每个节点的入度。
创建一个入度为0的节点队列。
当队列不为空时,执行以下操作:
从队列中取出一个节点,将其加入拓扑排序结果列表。
对于该节点的每个相邻节点,将其入度减1。
如果某个相邻节点的入度变为0,则将其加入队列。
如果拓扑排序结果列表中的节点数量与图中的节点数量相等,则排序成功;否则,图中存在环,无法进行拓扑排序。
2. 深度优先搜索(DFS)算法
DFS算法是一种递归的拓扑排序方法。它利用深度优先搜索遍历图的节点,并在回溯时记录节点的访问顺序(但需要进行一些调整以确保正确的拓扑顺序)。
具体步骤如下:
对每个未访问的节点,执行深度优先搜索。
在访问一个节点时,将其标记为临时访问(即正在访问中)。
递归地访问该节点的所有相邻节点。
当所有相邻节点都被访问完毕后,将该节点标记为永久访问(即已完成访问),并将其加入拓扑排序结果列表的开头(注意是开头,因为DFS是后序遍历,所以需要将节点逆序加入结果列表以得到正确的拓扑顺序)。
如果在访问过程中遇到一个已经标记为临时访问的节点,则说明图中存在环,无法进行拓扑排序。
四、拓扑排序的应用实例
为了更好地理解拓扑排序的实际应用,让我们通过一个具体的例子来说明。
假设我们有一个简单的软件开发项目,其中包含以下任务及其依赖关系:
A:编写代码
B:测试代码
C:设计UI
D:集成UI
E:编写文档
依赖关系如下:
A必须在B之前完成。
C必须在D之前完成。
B和D都必须在E之前完成。
根据这些依赖关系,我们可以构建一个有向图,并使用拓扑排序来确定任务的执行顺序。
使用Kahn算法或DFS算法,我们可以得到以下可能的拓扑排序结果:
A -> B -> C -> D -> E
这个顺序满足了所有的依赖关系,因此是一个有效的拓扑排序。
五、拓扑排序的局限性与挑战
尽管拓扑排序在解决许多实际问题时表现出色,但它也面临着一些局限性和挑战。
首先,拓扑排序只能应用于有向无环图(DAG)。如果图中存在环,则无法进行拓扑排序。在实际应用中,这要求我们在进行拓扑排序之前,必须确保图是无环的。
其次,对于大规模的有向图,拓扑排序的计算复杂度可能较高。特别是当图非常密集或节点数量巨大时,算法的性能可能会成为瓶颈。因此,在实际应用中,我们需要根据具体问题的规模和复杂度来选择合适的算法和优化策略。
最后,拓扑排序的结果可能不是唯一的。对于有多个入度为0的节点的情况,不同的算法或实现方式可能会产生不同的排序结果。这要求我们在使用拓扑排序时,要理解并接受其结果的多样性。
六、结语
有向图的拓扑排序是一项强大的技术,它为我们提供了一种按照依赖关系遍历图节点的有效方法。通过理解拓扑排序的基本概念、实现方法和应用实例,我们可以更好地解决各种实际问题中的依赖关系问题。同时,我们也需要注意到拓扑排序的局限性和挑战,并在实际应用中采取相应的措施来应对这些问题。
无论是软件开发、编译器设计还是数据库系统等领域,拓扑排序都发挥着不可替代的作用。它以其独特的魅力和广泛的应用前景,成为了计算机科学和数学领域中一颗璀璨的明珠。随着技术的不断进步和应用领域的不断拓展,拓扑排序将继续在解决复杂网络结构问题中发挥着越来越重要的作用。
- 上一篇: 如何在Word中打出点点点(省略号)?
- 下一篇: 和平精英怎么更改男女性别?
-
 如何轻松绘制网络拓扑图资讯攻略11-01
如何轻松绘制网络拓扑图资讯攻略11-01 -
 轻松学会:网线制作全攻略,包括接头接线与线序排序技巧资讯攻略11-20
轻松学会:网线制作全攻略,包括接头接线与线序排序技巧资讯攻略11-20 -
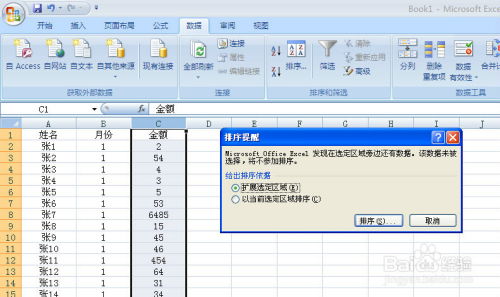 Excel技巧提升:确保数据排序时内容保持有序的方法资讯攻略02-04
Excel技巧提升:确保数据排序时内容保持有序的方法资讯攻略02-04 -
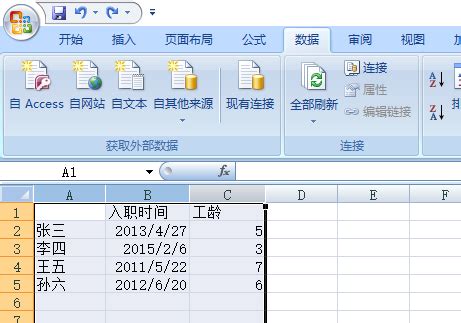 Excel表格排序的高效三绝招资讯攻略10-27
Excel表格排序的高效三绝招资讯攻略10-27 -
 Excel如何进行分类汇总?资讯攻略11-18
Excel如何进行分类汇总?资讯攻略11-18 -
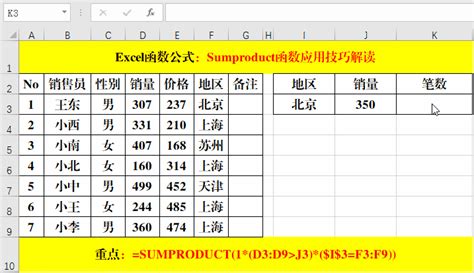 Q&A:掌握Sumproduct函数的6大经典应用技巧,不容错过!资讯攻略11-23
Q&A:掌握Sumproduct函数的6大经典应用技巧,不容错过!资讯攻略11-23












