如何计算相关系数r?
相关系数r的计算公式解析

在统计学中,相关系数r是一种用于衡量两个变量之间线性相关程度的指标。它揭示了当一个变量发生变化时,另一个变量将如何变化,以及变化的强度和方向。对于那些对数据分析、统计学或科学研究感兴趣的读者来说,了解相关系数r的计算公式及其背后的逻辑是至关重要的。

相关系数r的取值范围在-1到1之间。当r的值为1时,表示两个变量之间存在完全正相关的关系,即一个变量的增加会导致另一个变量的增加,反之亦然。当r的值为-1时,表示两个变量之间存在完全负相关的关系,即一个变量的增加会导致另一个变量的减少。而当r的值为0时,则表示两个变量之间不存在线性相关关系,即它们的取值变化是独立的。
那么,如何计算相关系数r呢?其核心公式为:
r = (∑(x - x̄)(y - ȳ)) / √(∑(x - x̄)²∑(y - ȳ)²)
这个公式看起来可能有些复杂,但我们可以分步骤地解析它:
1. 计算平均值:
x̄ 是变量x的平均值,计算公式为 ∑x / n,其中∑x表示变量x所有值的总和,n表示观测值的数量。
ȳ 是变量y的平均值,计算公式为 ∑y / n,其中∑y表示变量y所有值的总和。
2. 计算偏差:
对于每个x值,计算其与平均值的偏差,即 x - x̄。
对于每个y值,同样计算其与平均值的偏差,即 y - ȳ。
3. 计算偏差乘积的和:
将每对偏差值相乘,然后求这些乘积的总和,即 ∑(x - x̄)(y - ȳ)。
4. 计算偏差的平方和:
对于x的每个偏差值,计算其平方,然后求这些平方的总和,即 ∑(x - x̄)²。
对于y的每个偏差值,同样计算其平方,然后求这些平方的总和,即 ∑(y - ȳ)²。
5. 计算标准差乘积的平方根:
将x的偏差平方和与y的偏差平方和分别开方,然后求这两个标准差的乘积的平方根,即 √(∑(x - x̄)²∑(y - ȳ)²)。
6. 计算相关系数r:
最后,将偏差乘积的总和除以标准差乘积的平方根,得到相关系数r的值。
这个公式虽然看起来繁琐,但实际上它是对两个变量线性关系的一种量化表达。通过计算r值,我们可以快速了解两个变量之间的相关程度,从而做出更为准确的预测和决策。
除了上述的基本公式外,还有一些相关的概念和注意事项值得了解:
线性关系:相关系数r衡量的是两个变量之间的线性关系。如果两个变量之间的关系是非线性的(如二次函数、指数函数等),那么r值可能无法准确反映它们之间的关联程度。
样本相关系数与总体相关系数:上述公式计算的是样本相关系数,即基于有限数量的观测值所得出的结果。如果我们知道总体的所有观测值,那么可以计算出总体相关系数。但在大多数情况下,我们只能获取到样本数据,因此样本相关系数是我们更为关注的对象。
显著性检验:在计算得出r值后,通常还需要进行显著性检验。这是因为r值可能受到样本大小、数据分布等因素的影响而偏离真实值。通过显著性检验(如t检验),我们可以确定r值是否具有统计学意义上的显著性,从而更准确地评估两个变量之间的相关程度。
相关系数的应用:相关系数r在多个领域都有广泛的应用。例如,在市场营销中,商家可以通过计算不同产品销量之间的相关系数来制定促销策略;在金融领域,投资者可以通过计算不同资产收益率之间的相关系数来构建投资组合以分散风险;在医学研究中,研究人员可以通过计算药物疗效与患者症状改善程度之间的相关系数来评估药物的疗效等。
此外,还有一些相关指标与相关系数r密切相关,如决定系数(r²)、皮尔逊相关系数(当数据服从正态分布时)、斯皮尔曼秩相关系数(当数据不满足正态分布假设时)等。这些指标在不同的应用场景下具有各自的优势和局限性。
总的来说,相关系数r是一种强大的统计工具,它可以帮助我们量化两个变量之间的线性关系,从而为决策和分析提供有力的支持。通过深入理解和熟练掌握相关系数r的计算方法和应用场景,我们可以更好地利用数据来揭示事物之间的内在联系和规律。
- 上一篇: 全面掌握360浏览器搜索设置,优化您的浏览体验
- 下一篇: 花呗账户冻结?快速解冻指南!
-
 揭秘:5R照片尺寸全解析资讯攻略11-17
揭秘:5R照片尺寸全解析资讯攻略11-17 -
 RSD%的计算方法是什么?资讯攻略11-20
RSD%的计算方法是什么?资讯攻略11-20 -
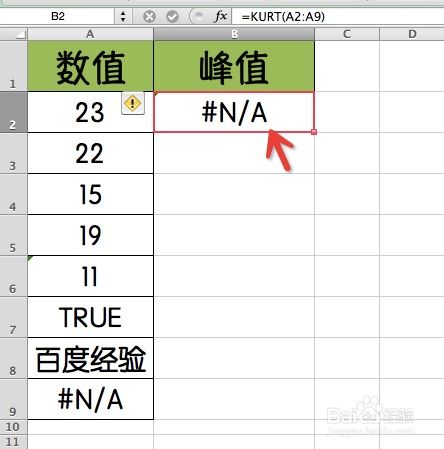 掌握KURT函数:轻松计算数据峰度资讯攻略02-04
掌握KURT函数:轻松计算数据峰度资讯攻略02-04 -
 如何在GeoGebra图形计算器中绘制爱心资讯攻略10-28
如何在GeoGebra图形计算器中绘制爱心资讯攻略10-28 -
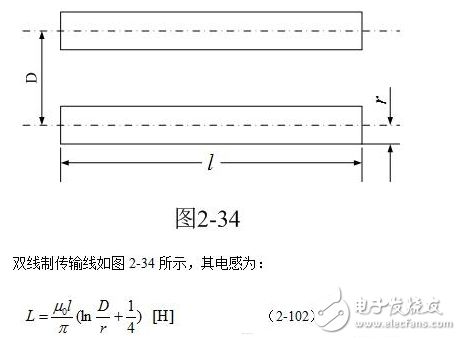 电感计算公式的具体形式资讯攻略01-17
电感计算公式的具体形式资讯攻略01-17 -
 土建工程中如何区分放坡系数与坡度?资讯攻略11-09
土建工程中如何区分放坡系数与坡度?资讯攻略11-09











