揭秘！圆柱侧面积的神奇等式，你不可不知的几何奥秘

在浩瀚的数学世界里，隐藏着无数奇妙而实用的秘密，而“圆柱的侧面积”这一话题，就像是一把钥匙，轻轻一转，就能打开一扇通往几何美学与实际应用相结合的大门。想象一下，从日常生活中常见的易拉罐、卷纸筒到宏伟的建筑结构，圆柱的身影无处不在，而理解其侧面积的计算，不仅能让我们更好地欣赏这些设计的美感，还能在解决实际问题时游刃有余。今天，就让我们一起踏上这场探索之旅，揭开圆柱侧面积神秘面纱的同时，也让这段旅程变得生动有趣。

圆柱的侧面积：从平凡到非凡的跨越

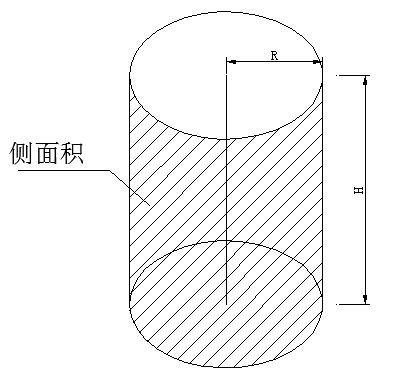
首先，让我们从最基本的定义出发。圆柱，这个简单而又经典的几何体，由两个平行的圆形底面和一个侧面组成，侧面展开后是一个矩形。这个看似平凡的构造，实则蕴含了无限的智慧与奥秘。那么，我们所说的“圆柱的侧面积”到底指的是什么呢？简而言之，它就是圆柱侧面那个“展开后的矩形”的面积。

走进几何的魔法世界

要计算圆柱的侧面积，我们不需要复杂的咒语，只需要掌握几个基本的几何公式和一个简单的想象过程。想象一下，你正手持一把锋利的剪刀，沿着圆柱侧面的一条母线（连接上下底面圆心的线段在侧面上的投影）缓缓剪开，圆柱的侧面便如魔法般展开成了一个矩形。这个矩形的长，实际上就是圆柱底面的周长，而宽，则是圆柱的高。

周长与高的交响曲

现在，让我们来一场关于“周长”与“高”的交响乐。圆柱底面的周长，是圆的基本属性之一，计算公式为2πr（其中r为圆的半径，π是一个神奇的数，约等于3.14159...）。而圆柱的高，则是从底面到顶面的垂直距离，直接测量即可得知。这两个数值相乘，便得到了我们梦寐以求的圆柱侧面积公式：S = 2πrh。

生活中的圆柱侧面积

理论知识总是枯燥的，但一旦将它们应用于生活，就会变得生动而有趣。比如，当你需要为家里的卷纸筒制作一个精美的外套时，首先就需要计算卷纸筒的侧面积，以确保外套能完美贴合。又或者，设计师在设计易拉罐时，也需要精确计算侧面积，以便在不浪费材料的同时，让包装更加美观和吸引人。此外，在建筑领域，圆柱形的塔楼、柱子等结构的设计，也离不开对侧面积的精准把握。

探索背后的故事

每一个数学公式背后，都藏着一段段鲜为人知的故事。圆柱侧面积的计算公式，看似简单，实则是无数数学家长期探索与实践的结果。从古希腊的毕达哥拉斯学派开始，人类就一直在探索圆的奥秘，而圆柱作为圆的一种扩展形式，自然也成为了研究的重点。随着时间的推移，人们逐渐发现了圆柱侧面积与底面周长、高之间的巧妙关系，这一发现不仅丰富了几何学的内容，更为后续的数学、物理、工程等领域的发展奠定了坚实的基础。

动手实践，感受数学的魅力

理论学习之外，动手实践是加深理解、感受数学魅力的最佳途径。不妨找一个圆柱形的物品（如易拉罐、卷纸筒等），亲自动手测量其底面半径和高，然后利用所学公式计算出侧面积。当你看到自己的计算结果与实际情况相吻合时，那种成就感和喜悦感将是任何言语都无法替代的。

结语

通过这次关于“圆柱的侧面积”的探索之旅，我们不仅学到了一个实用的几何公式，更体会到了数学与生活之间的紧密联系。数学，不再是一门遥不可及的学科，而是我们认识世界、改造世界的有力工具。希望这次旅行能够激发你对数学的兴趣和热爱，让你在未来的日子里，继续带着好奇心和探索精神，在数学的海洋中遨游，发现更多未知的美好。