揭秘！直角三角形面积的神奇计算法，一学就会的实用公式

直角三角形，作为几何学中基础而重要的图形之一，其面积的计算是许多学科领域如数学、物理、工程等不可或缺的基础知识。掌握直角三角形面积的计算公式，不仅能够帮助我们解决日常生活中的实际问题，还是深入理解更复杂几何与代数概念的基石。下面，就让我们一起探索这个既简单又强大的数学工具——直角三角形的面积计算公式。

直角三角形的定义与特征

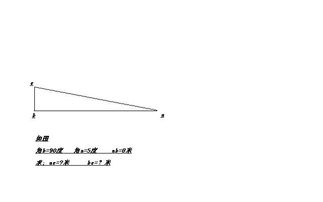
首先，明确直角三角形的定义：一个三角形中，如果有一个角为90度（直角），则这个三角形被称为直角三角形。它有两个锐角（小于90度的角）和一个直角（90度的角）。在直角三角形中，与直角相邻的两条边被特别称为直角边，而斜边则是连接两个锐角的边，也是这个三角形中最长的边。

面积计算公式的推导

直角三角形的面积计算公式相对直观且易于推导。我们知道，任意三角形的面积可以通过底和高来计算，而直角三角形中，任何一条直角边都可以作为底，另一条直角边则作为相应的高。基于这个原理，我们可以得出直角三角形面积的计算公式。

假设直角三角形的两条直角边长度分别为a和b，斜边长度为c（注意，c在面积计算中不直接使用，但在某些问题中，如利用勾股定理求解时，c是重要的）。根据三角形面积的一般计算方法，面积S等于底乘以高的一半，即：

\[ S = \frac{1}{2} \times \text{底} \times \text{高} \]

在直角三角形中，选择任意一条直角边作为底，另一条直角边作为高，代入公式得：

\[ S = \frac{1}{2} \times a \times b \]

这就是直角三角形面积的计算公式。它简洁明了，只需知道直角三角形的任意两条直角边的长度，即可迅速计算出其面积。

实际应用举例

例1：房屋建造的初步规划

假设你在进行房屋设计时，需要规划一个直角三角形的花坛。已知花坛的两条直角边长度分别为3米和4米，你可以直接应用上述公式计算出花坛的面积：

\[ S = \frac{1}{2} \times 3 \times 4 = 6 \text{平方米} \]

这样，你就可以根据面积来估算所需的花卉数量、土壤量等，为后续的建造工作提供依据。

例2：测量与计算

在地理测绘、土木工程或日常生活中，我们经常需要测量和计算直角三角形的面积。比如，一块土地的形状接近直角三角形，你可以通过测量其两条直角边的长度，然后利用公式计算出大致的面积，这对于土地规划、建筑设计等都具有重要意义。

进阶应用：勾股定理与面积的关系

虽然直接计算面积时不需要用到斜边c，但了解勾股定理（$a^2 + b^2 = c^2$）可以帮助我们解决更复杂的问题，比如当只知道斜边和一条直角边的长度时，如何求出另一条直角边和三角形的面积。通过勾股定理，我们可以先求出未知的直角边长度，再应用面积公式进行计算。

结语

直角三角形的面积计算公式，作为几何学中的基本工具，不仅在数学学习中占据重要地位，也是连接理论知识与实际应用的桥梁。掌握这一公式，不仅能够让我们在解决具体问题时更加得心应手，还能激发我们对几何世界的无限好奇与探索欲。无论是学习、工作还是生活中的方方面面，直角三角形及其面积计算公式都发挥着不可替代的作用。希望这篇文章能够帮助你更好地理解和应用这一重要知识点，开启你探索数学世界的奇妙之旅。