二次根式的性质详解
二次根式性质的深度解析

在数学领域中,二次根式是代数的一个重要组成部分,它涉及到对平方根运算的理解和运用。所谓二次根式,通常是指形如√a(a≥0)的代数式,其中a是被开方数,而√则是开方运算的符号。当我们深入探索二次根式的性质时,会发现其背后隐藏着丰富的数学原理和广泛的应用价值。

一、定义与基本概念
二次根式的基础是平方根的概念。平方根是一个数,它的平方等于给定的数。例如,4的平方根是2,因为2的平方等于4。在二次根式中,这个概念被扩展到更一般的形式,即√a表示a的平方根,其中a是非负实数。如果a是负数,那么在实数范围内,√a是没有意义的,但在复数范围内可以找到其解。
二、基本性质
1. 非负性:
对于任何非负实数a,其平方根√a都是非负的。这是因为在实数范围内,我们只考虑正的平方根。这一性质保证了二次根式在运算中的稳定性和一致性。
2. 算术性质:
二次根式具有一系列的算术性质,这些性质是我们在进行二次根式运算时需要遵循的。例如,√(ab) = √a × √b(其中a≥0,b≥0),这被称为二次根式的乘法性质。同样,√(a/b) = √a / √b(其中a≥0,b>0),这是二次根式的除法性质。此外,还有(√a)^2 = a(其中a≥0),这是二次根式的平方性质。
3. 化简性质:
二次根式可以进一步化简,以得到最简形式。例如,如果a是一个完全平方数,那么√a可以化简为相应的整数。更一般地,如果a可以表示为两个整数的乘积,且其中一个整数是完全平方数,那么√a也可以化简。化简二次根式是数学中的一个重要技能,它有助于我们更简洁地表示和计算二次根式。
4. 共轭性质:
对于任何一个二次根式√a(其中a>0),都存在一个与之共轭的二次根式-√a。这两个二次根式在运算中具有一些特殊的性质,例如它们的乘积是一个负数。共轭二次根式的概念在解决某些数学问题时非常有用。
三、运算法则
1. 加法与减法:
二次根式的加法与减法运算通常涉及将具有相同被开方数的二次根式进行合并。例如,对于√2 + 3√2,我们可以将它们合并为4√2。同样地,对于√3 - 2√3,我们可以得到-√3。在进行加法与减法运算时,需要注意保持二次根式的形式不变,即只合并具有相同被开方数的项。
2. 乘法与除法:
二次根式的乘法与除法运算基于其算术性质。例如,对于√a × √b(其中a≥0,b≥0),我们可以直接将其化简为√(ab)。同样地,对于√a / √b(其中a≥0,b>0),我们可以将其化简为√(a/b)。在进行乘法与除法运算时,需要注意保持运算的优先级和顺序,以确保结果的准确性。
3. 乘方与开方:
二次根式的乘方运算通常涉及将二次根式作为底数进行幂运算。例如,(√a)^n(其中a≥0,n为正整数)表示将√a进行n次幂运算。同样地,对于形如a^(1/2)(其中a≥0)的表达式,我们可以将其化简为√a。在进行乘方运算时,需要注意幂运算的优先级和规则,以确保结果的正确性。另一方面,开方运算则是乘方运算的逆运算,它涉及将一个数进行平方根运算以得到其平方根。
四、特殊情况的处理
1. 零的平方根:
根据二次根式的定义,0的平方根是0。这是因为0的平方等于0,所以0是自身的平方根。这一性质在二次根式的运算中具有重要意义,因为它保证了二次根式在运算中的连续性和完整性。
2. 负数的平方根:
在实数范围内,负数的平方根是没有意义的。然而,在复数范围内,我们可以找到负数的平方根。例如,-1的平方根是±i(其中i是虚数单位,满足i^2 = -1)。这一性质扩展了二次根式的应用范围,使其能够处理更复杂的数学问题。
3. 完全平方数的平方根:
对于完全平方数(即可以表示为某个整数的平方的数),其平方根可以化简为相应的整数。例如,对于9(即3的平方),其平方根是3。这一性质在化简二次根式时非常有用,因为它可以帮助我们快速找到二次根式的最简形式。
五、应用与实例
二次根式在数学和物理学中具有广泛的应用。例如,在几何学中,二次根式可以用于计算图形的面积和周长;在物理学中,二次根式可以用于描述物体的速度和加速度等运动状态。此外,二次根式还在经济学、工程学等领域中发挥着重要作用。
以几何学为例,假设我们有一个边长为a的正方形,那么它的面积就是a^2。如果我们想要知道这个正方形的边长是多少,就需要对其进行开方运算,即求解√(a^2)。根据二次根式的性质,我们知道√(a^2) = a(其中a≥0),所以正方形的边长就是a。
再来看一个物理学中的例子。假设一个物体以恒定的加速度a进行直线运动,并且它的初速度为0。那么,在t秒后,它的速度v就是at(根据速度-时间公式v = at)。如果我们想要知道这个物体在t秒内的位移s是多少,就需要使用位移-时间公式s = (1/2)at^2。在这里,(1/2)at^2就是一个二次根式(虽然它看起来不像一个标准的二次根式形式,但我们可以将其看作√[(1/4)a^2t^4]的平方,从而将其与二次根式联系起来)。通过求解这个二次根式,我们可以得到物体在t秒内的位移s。
综上所述,二次根式是数学中的一个重要概念,它具有丰富的性质和广泛的应用价值。通过深入理解二次根式的性质和运用技巧,我们可以更好地解决各种数学问题,并将这些知识应用到实际生活中去。
- 上一篇: 如何将百度APP中的视频下载到手机
- 下一篇: FGO攻略:伊凡雷帝击败全解析,轻松制胜秘诀!
-
 二次根式乘除法的规则是什么?资讯攻略01-13
二次根式乘除法的规则是什么?资讯攻略01-13 -
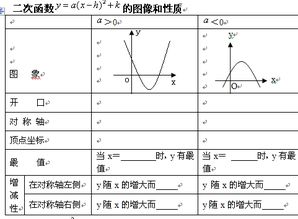 探索二次函数:图像之美与性质之谜资讯攻略11-08
探索二次函数:图像之美与性质之谜资讯攻略11-08 -
 十字相乘法因式分解步骤详解资讯攻略01-19
十字相乘法因式分解步骤详解资讯攻略01-19 -
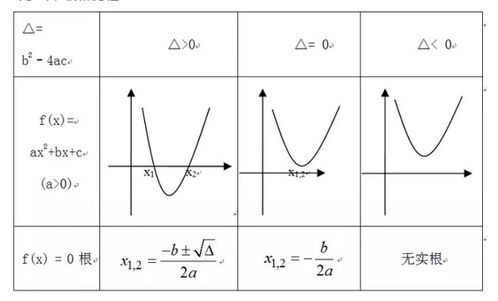 二次函数的顶点如何求解?资讯攻略12-07
二次函数的顶点如何求解?资讯攻略12-07 -
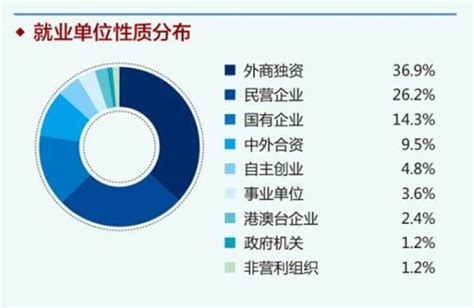 揭秘:单位性质与经济类型的多样化分类详解资讯攻略02-17
揭秘:单位性质与经济类型的多样化分类详解资讯攻略02-17 -
 LDPE材料详解资讯攻略10-28
LDPE材料详解资讯攻略10-28












