二次函数的顶点如何求解？

在数学的世界里，二次函数如同一座桥梁，连接着代数与几何的深邃之美。它不仅是初中数学课程中的重要内容，也是高中乃至大学数学中不可或缺的一部分。而二次函数的顶点，则是这座桥梁上的一颗璀璨明珠，它蕴含着函数图像的最高点或最低点，是理解函数性质、解决实际问题的关键所在。本文旨在深入探讨二次函数的顶点，帮助读者全面理解这一概念。

一、二次函数的基本形式

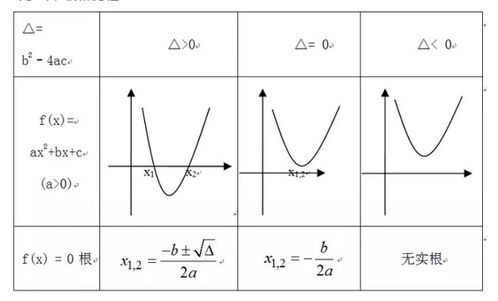
二次函数，顾名思义，其函数表达式中变量的最高次数为2。一般地，二次函数可以表示为y=ax²+bx+c（a≠0）的形式，其中a、b、c为常数，且a决定了函数的开口方向：当a>0时，函数图像开口向上；当a<0时，函数图像开口向下。b和c则与函数的对称轴和顶点位置有关。

二、顶点的意义

二次函数的顶点，是函数图像上最特殊的一点。它不仅决定了函数图像的最高点（当函数开口向下时）或最低点（当函数开口向上时），还揭示了函数图像的对称性质。对于任何给定的二次函数y=ax²+bx+c，其顶点坐标（h,k）都满足特定的关系，这种关系使得我们可以通过简单的代数运算找到顶点，而无需绘制整个函数图像。

三、顶点的求解方法

1. 公式法

求解二次函数顶点的最直接方法是使用顶点公式。对于一般形式的二次函数y=ax²+bx+c，其顶点坐标（h,k）可以通过以下公式求得：

h=-b/(2a)

k=c-b²/(4a)

这个公式来源于二次函数的完全平方公式。通过配方，我们可以将一般形式的二次函数转化为顶点式y=a(x-h)²+k，从而直接读出顶点坐标（h,k）。

2. 几何法

除了公式法，我们还可以通过几何方法找到二次函数的顶点。由于二次函数的图像是一条抛物线，而抛物线是关于其对称轴对称的，因此我们可以通过找到抛物线与x轴的交点（即解方程ax²+bx+c=0），然后利用对称轴的性质来确定顶点的位置。不过，这种方法相对繁琐，不如公式法直观和高效。

3. 图像法

对于能够使用图形计算器或绘图软件的读者来说，通过绘制二次函数的图像来观察顶点也是一种直观的方法。虽然这种方法依赖于技术工具，但它能够直观地展示函数图像的全貌，有助于加深对二次函数性质的理解。

四、顶点的应用

二次函数的顶点在解决实际问题中具有广泛的应用。例如，在物理学中，当研究物体在重力作用下的自由落体运动时，其运动轨迹可以看作是一条抛物线，而顶点的位置则对应着物体达到的最高点；在经济学中，二次函数常用于描述成本、收益等经济变量与产量之间的关系，而顶点的位置则揭示了最优产量和最大利润；在工程学中，二次函数可用于设计抛物面天线、桥梁等结构，顶点的位置对于结构的稳定性和美观性至关重要。

五、顶点的性质

二次函数的顶点不仅是一个具体的点，它还承载着丰富的数学性质。以下是一些关于顶点的重要性质：

1. 对称性：二次函数的图像关于其对称轴对称，而对称轴的方程正是x=h，其中h是顶点的x坐标。

2. 极值性：当二次函数开口向上时，顶点是其图像上的最低点，函数值达到最小值；当二次函数开口向下时，顶点是其图像上的最高点，函数值达到最大值。

3. 唯一性：对于给定的二次函数，其顶点坐标是唯一的，这保证了函数图像的唯一性和确定性。

4. 可变性：通过改变二次函数中的a、b、c三个参数，我们可以得到不同的二次函数图像，其顶点的位置也会相应改变。

六、顶点的拓展思考

在深入理解了二次函数顶点的基本概念、求解方法和应用之后，我们还可以进一步拓展思考。例如，对于更复杂的二次函数形式（如含有根号、分数或多项式的二次函数），其顶点的求解方法是否仍然适用？如何利用顶点公式解决实际问题中的最优化问题？此外，二次函数的顶点与函数的单调性、最值等性质之间有何内在联系？这些问题不仅有助于深化我们对二次函数的理解，还能激发我们对数学世界的探索热情。

七、结语

二次函数的顶点，作为连接代数与几何的桥梁，不仅在数学学科内部扮演着重要角色，还在物理学、经济学、工程学等多个领域发挥着重要作用。通过本文的介绍，我们希望能够帮助读者全面理解二次函数顶点的概念、求解方法和应用，激发对数学的兴趣和热爱。在未来的学习和生活中，让我们继续探索数学的奥秘，用数学的眼光观察世界，用数学的语言描述世界，