如何绘制钝角三角形的高？

在探讨几何学中钝角三角形的性质时，一个常见且基础的问题是：“钝角三角形的高怎么画？”这一问题不仅考验着我们对三角形基本概念的理解，也要求我们掌握作图的基本技巧。下面，我们将通过详细的步骤和解释，来阐述如何在钝角三角形中准确地画出其高。

引言

钝角三角形，顾名思义，是三个角中有一个角大于90°的三角形。与锐角三角形和直角三角形相比，钝角三角形的形状显得更为“宽阔”或“扁平”。在几何学习中，高是一个重要的概念，它指的是从一个顶点到它所对的边（或该边的延长线）的垂线段的长度。对于钝角三角形而言，由于至少有一个角是钝角，其高的画法会稍有不同，特别是当高不直接落在对边上时。

钝角三角形高的定义与性质

在钝角三角形中，高的定义依然是从一个顶点出发，垂直于它所对的边（或该边的延长线）的线段。这个定义包含了两种情况：

1. 当高落在对边上时：如果钝角三角形的某个顶点恰好使得从该顶点出发的高能够直接落在对边上，那么画法与锐角三角形或直角三角形类似。这种情况相对较少见，但并非不可能。

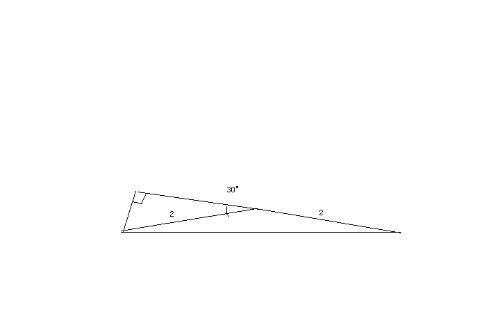
2. 当高落在对边的延长线上时：更常见的情况是，从钝角的两个非钝角顶点出发的高会落在对边的延长线上。这是因为钝角的存在使得从该角顶点出发的垂线无法直接到达对边，而必须“越过”三角形，落在其延长线上。

画法步骤

以下是绘制钝角三角形高的具体步骤，以从非钝角顶点出发的高为例（假设该顶点为A，其对边为BC）：

1. 确定顶点与对边：首先，明确钝角三角形的三个顶点（记为A、B、C）和要画高的顶点A所对的边BC。

2. 使用直尺和圆规：准备好作图工具，主要是直尺和圆规。直尺用于画直线，圆规则用于确定长度和角度。

3. 以A为圆心，适当长度为半径画弧：使用圆规，以顶点A为圆心，选择一个合适的半径（不宜过长或过短，以能清晰显示与BC边的交点或延长线的交点为宜），在A的两侧分别画两条弧。

4. 找到与BC边或延长线的交点：继续用圆规，以上一步中在BC边或BC延长线上与弧相交的两个点（记为D、E，其中D可能在BC上，E则在BC的延长线上）为圆心，再次使用相同的半径画弧。这两段新弧将在BC的上方或下方相交于一点（记为F）。

5. 连接AF：使用直尺连接顶点A与交点F，线段AF即为从顶点A出发的高。注意，如果F点在BC的延长线上，那么AF将是落在BC延长线上的高。

6. 标记与说明：在图中清晰地标出高AF，并可以标注其长度（如果已知或需要计算）和角度信息（如∠AFC为直角）。

应用与拓展

掌握钝角三角形高的画法，不仅有助于我们更深入地理解三角形的性质，还为后续学习如面积计算、三角函数应用等打下了坚实的基础。例如，利用钝角三角形的高，我们可以轻松地通过“底乘以高再除以二”的公式计算其面积，即便在不知道具体边长的情况下，也可以通过测量或计算高和对应底边的长度来估算。

此外，钝角三角形高的画法还与许多实际问题紧密相关，如建筑设计中的稳定性分析、工程测量中的角度校正等。通过将这些理论知识应用于实际情境中，我们可以更加深刻地体会到几何学在日常生活中的重要性。

结语

综上所述，钝角三角形高的画法虽然看似复杂，但只要掌握了正确的步骤和技巧，便能轻松应对。这一过程不仅锻炼了我们的空间想象能力和作图能力，也加深了我们对三角形及其性质的理解。希望本文的讲解能够帮助你更好地掌握这一知识点，并在未来的学习和生活中灵活运用。