如何绘制莱洛三角形？

探索奇妙的几何世界：如何绘制莱洛三角形

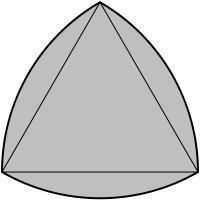
在几何学的广阔天地里，有许多令人惊叹的形状和图案，其中莱洛三角形（Reuleaux Triangle）以其独特的外观和性质吸引着无数数学爱好者和设计师的目光。莱洛三角形是一种定宽曲线形成的图形，它的每个顶点都是由一个圆弧构成的，这些圆弧的半径相等，并且互相外切。这种形状不仅在数学上具有独特的地位，还在工程设计和实际应用中发挥着重要作用。那么，如此独特的莱洛三角形究竟是如何绘制的呢？接下来，我们就来一起探索这个奇妙的几何世界。

一、准备工具

要绘制莱洛三角形，首先需要准备好一些基本的绘图工具。这些工具包括：

圆规：用于绘制圆弧和确定圆的半径。

直尺：用于测量和绘制直线段。

铅笔：用于勾勒轮廓和绘制细节。

纸张：选择一张质地适中、大小适宜的纸张进行绘图。

确保这些工具齐备并摆放整齐后，我们就可以开始绘制莱洛三角形了。

二、确定关键点

绘制莱洛三角形的第一步是确定其关键点。这些关键点包括莱洛三角形的三个顶点和三个圆弧的圆心。由于莱洛三角形的每个顶点都是由一个圆弧构成的，因此我们需要先确定这些圆弧的圆心和半径。

1. 选择半径：首先，我们需要在纸张上选择一个适当的半径R。这个半径将决定莱洛三角形的大小。使用圆规，我们在纸张上画出一个半径为R的圆，作为辅助图形。

2. 确定圆心：接下来，我们在圆上选择三个等间距的点作为莱洛三角形圆弧的圆心。这些点可以通过将圆分成三等分来找到。使用直尺和圆规，我们可以轻松地实现这一点。

3. 标记顶点：在确定了圆心之后，我们需要找到莱洛三角形的三个顶点。这些顶点位于以圆心为起点、半径为R的圆弧上，并且与相邻圆弧的圆心相连。使用圆规，我们在每个圆弧上找到与相邻圆心相切的点，并标记为顶点。

三、绘制圆弧

在确定了关键点之后，我们就可以开始绘制莱洛三角形的圆弧了。

1. 绘制第一个圆弧：选择第一个圆心，并使用圆规以该圆心为起点、半径为R绘制一个圆弧。这个圆弧将延伸到与相邻圆弧的圆心相切的位置。

2. 绘制第二个圆弧：接着，选择第二个圆心，并以同样的半径绘制第二个圆弧。这个圆弧将与第一个圆弧在第一个顶点处相切，并延伸到与第三个圆弧的圆心相切的位置。

3. 绘制第三个圆弧：最后，选择第三个圆心，并以同样的半径绘制第三个圆弧。这个圆弧将与第二个圆弧在第二个顶点处相切，并返回到第一个圆弧的起点处，与第一个圆弧在第三个顶点处相切。

完成这三个圆弧的绘制后，我们就得到了一个完整的莱洛三角形。

四、优化和检查

绘制完莱洛三角形后，我们需要进行一些优化和检查，以确保其准确性和美观性。

1. 检查相切性：首先，我们需要检查每个圆弧是否正确地与相邻圆弧相切。如果发现有任何不相切的地方，我们需要进行调整，以确保莱洛三角形的完整性。

2. 优化轮廓：接下来，我们可以使用铅笔轻轻地勾勒出莱洛三角形的轮廓线。这条轮廓线将穿过每个圆弧的顶点，并形成一个封闭的图形。通过优化轮廓线，我们可以使莱洛三角形的形状更加清晰和美观。

3. 添加细节：最后，我们可以根据需要添加一些细节和标注。例如，我们可以在莱洛三角形的每个顶点处标记一个小圆点，以突出其位置；或者我们可以在图纸上添加一些注释和说明，以帮助他人更好地理解我们的绘图过程。

五、实际应用与意义

莱洛三角形不仅在几何学上具有独特的地位，还在许多实际应用中发挥着重要作用。

1. 机械设计：在机械设计中，莱洛三角形常被用作定宽曲线的典型例子。由于其具有恒定的宽度特性，莱洛三角形在制造某些类型的齿轮、轴承和连接件时非常有用。

2. 建筑设计：在建筑设计中，莱洛三角形的独特形状和对称性为建筑师提供了灵感来源。他们可以利用这种形状来设计具有独特外观和结构的建筑作品。

3. 艺术创作：在艺术创作中，莱洛三角形也被广泛运用。艺术家们可以利用其独特的形状和轮廓来创作具有现代感和艺术感的作品。

此外，莱洛三角形还在数学教育和科普领域发挥着重要作用。通过学习和绘制莱洛三角形，学生们可以深入了解几何学的奥秘和魅力，并培养他们的空间想象力和创造力。

六、结语

通过以上的介绍，我们了解了如何绘制莱洛三角形以及其在实际应用中的意义。莱洛三角形以其独特的形状和性质在几何学、机械设计和艺术创作等领域中发挥着重要作用。希望这篇文章能够帮助你更好地理解和掌握莱洛三角形的绘制方法，并激发你对几何学世界的好奇心和探索欲。在未来的学习和实践中，不妨尝试将莱洛三角形应用于更多的领域和场景中，去发现它所带来的无限可能和惊喜吧！