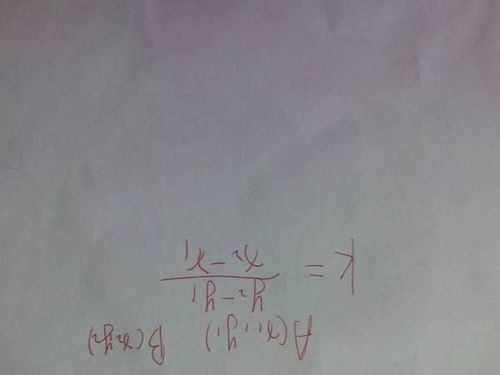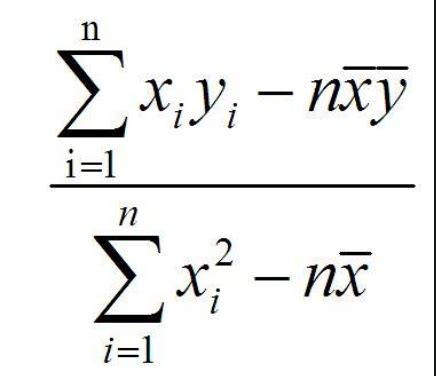斜率的计算公式是什么?
在数学的广阔领域中,斜率是一个至关重要的概念,尤其在解析几何和微积分中扮演着举足轻重的角色。它不仅能够帮助我们描述直线在平面直角坐标系中的倾斜程度,还能进一步揭示函数图像的变化规律。本文旨在深入探讨斜率的定义、公式、计算方法以及其在各种情境下的应用,为读者提供一个全面而详尽的理解框架。

一、斜率的定义
斜率,简而言之,是描述一条直线倾斜程度的量度。在平面直角坐标系中,直线由无数个点组成,而这些点都遵循一定的线性关系,即满足直线方程。斜率正是用来量化这种线性关系倾斜程度的数值。具体来说,斜率反映了直线沿y轴上升或下降的速度相对于沿x轴移动的速度。

二、斜率的公式
斜率的计算公式是理解这一概念的核心。对于任意两点P1(x1, y1)和P2(x2, y2)在平面直角坐标系上确定的直线,其斜率m可以通过以下公式计算得出:

m = (y2 - y1) / (x2 - x1)
这个公式直观地表明了斜率是如何通过两点的坐标差来定义的。当x2不等于x1时,即两点横坐标不相同时,我们可以直接应用上述公式。然而,当x1等于x2时,即两点横坐标相同、纵坐标不同,表示这是一条垂直于x轴的直线,此时斜率不存在(或者说斜率为无穷大),因为直线在任何一点上都没有明确的倾斜方向。
三、斜率的计算实例
为了更好地理解斜率公式的应用,我们可以通过几个具体的例子来加以说明。
例1:给定两点A(2, 3)和B(5, 7),求直线AB的斜率。
根据斜率公式,我们有:
m = (7 - 3) / (5 - 2) = 4 / 3
因此,直线AB的斜率为4/3。
例2:已知点C(-1, 4)和直线D的方程为y = 2x + 3,求过点C且与直线D平行的直线的斜率。
由于两直线平行,它们的斜率必须相等。直线D的斜率为2(从方程y = 2x + 3中直接读出),因此过点C的平行线的斜率也是2。这里虽然未直接使用斜率公式计算,但展示了斜率在判断两直线位置关系中的应用。
四、斜率的几何意义
斜率的几何意义在于它揭示了直线在平面上的倾斜程度。斜率为正表示直线从左下方斜向右上方倾斜;斜率为负则表示直线从左上方斜向右下方倾斜;斜率为0时,直线水平,不倾斜;斜率不存在(即无穷大)时,直线垂直。此外,斜率的大小还反映了直线倾斜的“陡峭”程度,斜率越大,直线越陡峭。
五、斜率在函数图像中的应用
在函数图像中,斜率同样扮演着重要的角色。对于一次函数y = kx + b(其中k为斜率,b为截距),斜率k不仅决定了直线的倾斜程度,还直接反映了函数值y随自变量x变化的速度。当k > 0时,函数是增函数,随着x的增加,y也增加;当k < 0时,函数是减函数,随着x的增加,y减少。斜率的大小还反映了这种增减的快慢,即函数的平均变化率。
对于更复杂的函数,如二次函数、指数函数、对数函数等,虽然它们的图像不再是直线,但斜率的概念仍然适用,只不过此时斜率是随着x的变化而变化的,称为导数。导数描述了函数在某一点附近的变化率,是微积分中的核心概念之一。
六、斜率在现实生活中的应用
斜率不仅在理论数学中占有重要地位,在实际生活中也有着广泛的应用。例如,在物理学中,斜率可以用来描述速度、加速度等物理量的变化;在经济学中,斜率可以反映供需曲线、成本效益分析等经济模型的斜率特征;在工程学中,斜率可以用于计算坡度、倾斜角等设计参数。此外,在数据分析、图像处理等领域,斜率也是不可或缺的工具。
七、斜率的计算注意事项
在使用斜率公式进行计算时,需要注意以下几点:
1. 确保分母(x2 - x1)不为0,即两点横坐标不能相同。
2. 斜率公式的应用不仅限于直线,对于曲线上的两点,虽然得到的斜率只能反映这两点间的局部倾斜程度,但在微分学的框架下,通过求极限可以得到曲线在某一点的切线斜率,即导数。
3. 在处理实际问题时,要根据具体情况选择合适的坐标系和单位,以确保计算结果的准确性和合理性。
八、结语
综上所述,斜率作为解析几何和微积分中的基本概念,不仅具有深刻的数学意义,而且在实际应用中发挥着重要作用。通过理解斜率的定义、掌握其计算公式、明确其几何意义和实际应用场景,我们可以更好地利用这一工具来分析和解决问题。无论是理论研究还是实际应用,斜率都是连接数学与现实世界的桥梁,值得我们深入学习和探索。
- 上一篇: 轻松掌握:如何打出单书名号
- 下一篇: Word文档页码设置教程
-
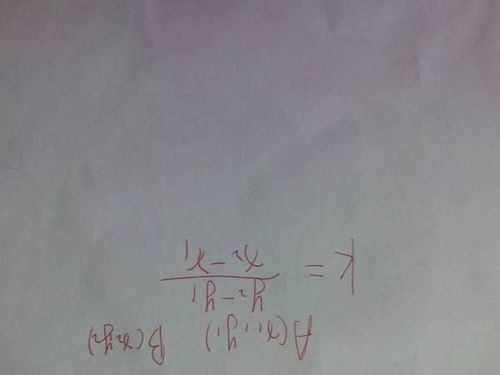 如何计算两点之间的斜率?资讯攻略11-18
如何计算两点之间的斜率?资讯攻略11-18 -
 资料分析中的比重计算公式是什么?资讯攻略11-08
资料分析中的比重计算公式是什么?资讯攻略11-08 -
 正方形周长的计算公式是什么资讯攻略11-01
正方形周长的计算公式是什么资讯攻略11-01 -
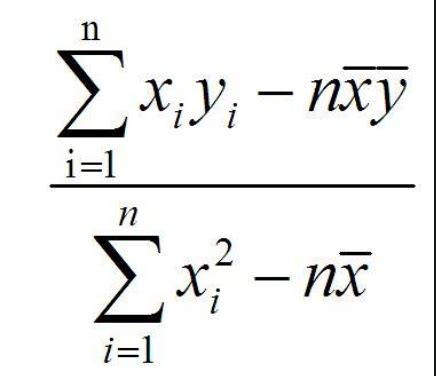 回归分析法的计算公式是什么?资讯攻略12-01
回归分析法的计算公式是什么?资讯攻略12-01 -
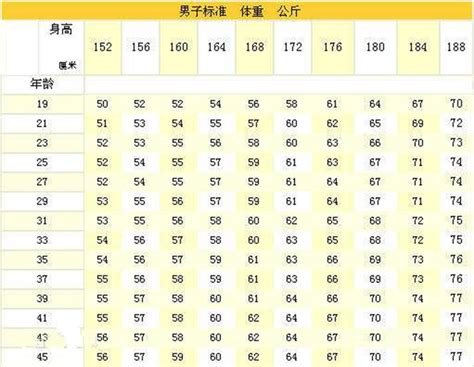 中考时计算身高与体重的公式是什么?资讯攻略11-23
中考时计算身高与体重的公式是什么?资讯攻略11-23 -
 半圆面积的计算公式是什么?资讯攻略10-29
半圆面积的计算公式是什么?资讯攻略10-29