如何计算两点之间的斜率？

在数学学习中，求解两点之间的斜率是一个基础而重要的概念。斜率，简而言之，描述的是一条直线倾斜的程度。当我们知道直线上的两个点时，可以通过一系列简单的计算来求出这条直线的斜率。以下是对“两点怎么求斜率”这一主题的详细探讨。

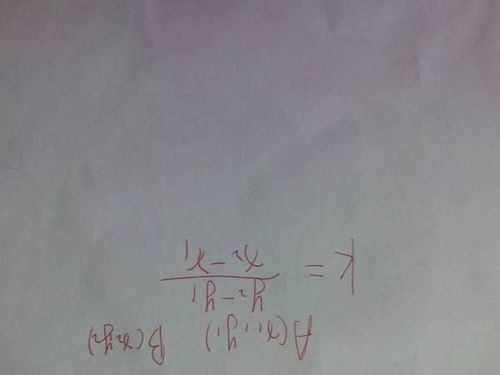
首先，我们需要明确什么是斜率。斜率（m）在几何学中定义为直线上升或下降的“陡峭”程度。它是直线倾斜角的正切值，通常用大写字母M或小写字母m表示。斜率的正负和大小能够告诉我们直线是上升还是下降，以及上升或下降的速度有多快。一个正的斜率表示直线从左下方斜向右上方，而负的斜率则表示直线从左上方斜向右下方。斜率的绝对值越大，直线的倾斜程度就越大，即直线越陡峭；斜率的绝对值越小，直线的倾斜程度就越小，即直线越平缓。

在求解两点之间的斜率时，我们通常使用所谓的“斜率公式”。这个公式是基于直线上任意两点的坐标来计算斜率的。假设我们有两个点A和B，其中点A的坐标为(x₁, y₁)，点B的坐标为(x₂, y₂)。根据斜率公式，我们可以得到：

m = (y₂ - y₁) / (x₂ - x₁)

这个公式告诉我们，要求出两点之间的斜率，我们只需要将这两点的y坐标差除以x坐标差即可。需要注意的是，这里的x₂和x₁、y₂和y₁必须是对应的，不能混淆。同时，我们还必须确保x₂ ≠ x₁，因为如果x₂ = x₁，那么分母就会为0，这是数学中不允许的。

在实际应用中，我们可以通过这个公式来解决各种问题。比如，如果我们知道一条直线经过点(3, 5)和点(6, 11)，我们就可以用斜率公式来求出这条直线的斜率。将这两个点的坐标代入公式，我们得到：

m = (11 - 5) / (6 - 3) = 6 / 3 = 2

所以，这条直线的斜率为2，表示它是一条从左下方斜向右上方，且倾斜程度较大的直线。

除了用斜率公式来求解斜率之外，我们还可以通过观察直线的图像或分析直线的性质来推测斜率的大小和正负。比如，如果一条直线看起来非常陡峭，并且从左下方斜向右上方，那么我们就可以推测它的斜率是一个较大的正数。相反，如果一条直线看起来非常平缓，并且从左上方斜向右下方，那么我们就可以推测它的斜率是一个较小的负数。

当然，在实际应用中，我们还需要注意一些特殊情况。比如，当一条直线是水平的时候，它的斜率不存在或为0。这是因为水平的直线不会上升也不会下降，所以它的倾斜程度可以认为是0。同样地，当一条直线是垂直的时候，它的斜率也不存在，但我们可以说它的斜率是无穷大。这是因为垂直的直线会直接上升或下降，没有任何倾斜的角度可言。

此外，在求解斜率时，我们还需要注意一些计算技巧。比如，为了避免分数形式的答案，我们可以尝试通过约分或乘除一个适当的数来得到一个整数或更简单的分数形式的答案。同时，在计算过程中，我们也要注意保持计算的准确性，避免因为计算错误而导致答案错误。

斜率不仅在数学中有重要的应用，而且在其他学科和现实生活中也有着广泛的应用。比如，在物理学中，斜率可以用来描述物体的速度或加速度；在经济学中，斜率可以用来描述供需曲线的斜率或边际效益的变化；在地理学中，斜率可以用来描述地形的陡峭程度或河流的流速等。因此，掌握求解两点之间斜率的方法对于我们理解和应用数学知识以及解决实际问题都是非常有帮助的。

总的来说，求解两点之间的斜率是一个简单而重要的数学技能。通过掌握斜率公式和相关的计算技巧，我们可以轻松地求出任意两点之间的斜率，并据此分析直线的倾斜程度和性质。同时，斜率也是连接数学和其他学科以及现实世界的桥梁之一，它可以帮助我们更好地理解和应用数学知识来解决实际问题。因此，在学习数学的过程中，我们应该注重掌握和理解斜率的概念和计算方法，以便在未来的学习和工作中能够灵活运用这一重要的数学工具。

在结束这篇文章之前，我想再强调一下求解两点之间斜率的重要性。无论是在数学学习中还是在其他学科和现实生活中，斜率都是一个非常有用的概念。它不仅可以帮助我们分析和理解各种现象和问题，而且还可以为我们提供解决问题的新思路和方法。因此，我们应该认真对待每一个数学概念和技能的学习，不断提高自己的数学素养和综合能力，以便在未来的学习和工作中能够更好地应对各种挑战和机遇。