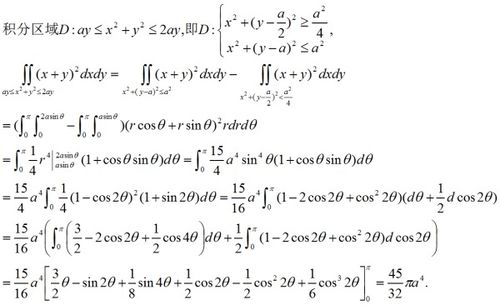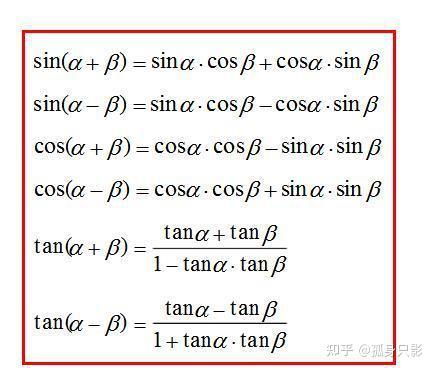如何轻松掌握二元一次方程的解题步骤?
在我们学习数学的过程中,二元一次方程是一个非常重要的知识点。它不仅是解决很多实际问题的工具,还是进一步学习其他数学知识的基础。然而,对于初学者来说,二元一次方程可能会显得有些复杂。别担心,今天我们就来详细讲解一下二元一次方程的解题步骤,让它变得通俗易懂。

首先,我们需要明白什么是二元一次方程。简单来说,二元一次方程就是含有两个未知数(我们通常用x和y来表示),并且这两个未知数的次数都是1的方程。它的标准形式通常写作ax + by = c,其中a、b、c是已知数,x和y是未知数。

接下来,我们就来一步一步地了解如何解二元一次方程。
第一步:列出方程组
在解决实际问题时,我们通常会得到两个或两个以上的二元一次方程,形成一个方程组。这些方程共同描述了问题的数学关系。
例如,假设我们有一个果园,种有苹果和梨。我们知道果园里总共有100棵树,其中苹果树每棵产50斤苹果,梨树每棵产30斤梨。我们还知道果园里总共产出了4600斤水果。那么,我们就可以列出以下两个方程:
1. 苹果树的数量 + 梨树的数量 = 100(因为总共有100棵树)
2. 苹果树产出的水果(50 * 苹果树的数量) + 梨树产出的水果(30 * 梨树的数量) = 4600(因为总共产出了4600斤水果)
用x表示苹果树的数量,y表示梨树的数量,这两个方程就可以写作:
1. x + y = 100
2. 50x + 30y = 4600
第二步:选择解题方法
对于二元一次方程组,我们有多种解题方法,其中最常用的有两种:代入法和消元法。
代入法:
1. 从方程组中选择一个方程,解出一个未知数的表达式(通常选择系数简单或容易解出的方程)。
2. 将这个未知数的表达式代入到另一个方程中,得到一个只含有一个未知数的一元一次方程。
3. 解这个一元一次方程,得到这个未知数的值。
4. 将得到的未知数的值代回到原来的方程中,求出另一个未知数的值。
消元法:
1. 观察方程组中的两个方程,通过对方程两边同时乘以或除以某个数,使得其中一个未知数的系数在两个方程中相等或互为相反数。
2. 将两个方程相减(或相加),消去一个未知数,得到一个只含有一个未知数的一元一次方程。
3. 解这个一元一次方程,得到这个未知数的值。
4. 将得到的未知数的值代回到原来的方程中,求出另一个未知数的值。
第三步:实际解题过程
我们以刚才果园的例子,用消元法来解题:
首先,我们有方程组:
1. x + y = 100
2. 50x + 30y = 4600
为了消去y,我们可以将第一个方程两边同时乘以30,得到:
30x + 30y = 3000
然后,我们将这个新得到的方程与第二个方程相减,得到:
(50x + 30y) - (30x + 30y) = 4600 - 3000
化简后得到:
20x = 1600
解这个一元一次方程,我们得到:
x = 80
最后,我们将x = 80代回到原来的第一个方程中,得到:
80 + y = 100
解这个方程,我们得到:
y = 20
所以,果园里有80棵苹果树和20棵梨树。
第四步:检查答案
得到答案后,我们还需要检查答案是否正确。这通常是通过将求得的x和y的值代回到原来的方程组中,看是否能够满足所有的方程。
将x = 80,y = 20代回到原方程组中,我们得到:
1. 80 + 20 = 100(满足)
2. 50 * 80 + 30 * 20 = 4000 + 600 = 4600(满足)
所以,我们的答案是正确的。
第五步:总结与反思
在解题过程中,我们可能会遇到一些困难,比如方程组的系数比较复杂,或者消元的过程中需要进行大量的计算。这时,我们需要保持耐心和细心,逐步进行运算和检查。
同时,我们还可以通过总结解题过程,发现一些规律和技巧。比如,在选择消元法时,我们通常选择系数相差较大的未知数进行消元,这样可以减少计算量。在代入法时,我们也可以选择容易解出的方程先解出一个未知数的表达式。
通过不断地练习和总结,我们可以逐渐提高解二元一次方程组的能力,更好地掌握这个重要的数学知识点。
总之,解二元一次方程组需要按照一定的步骤进行,包括列出方程组、选择解题方法、实际解题过程、检查答案以及总结与反思。只要我们掌握了这些步骤和技巧,就能够轻松解决各种二元一次方程组问题。希望这篇文章能够帮助你更好地理解二元一次方程的解题步骤,提高你的数学能力。
- 上一篇: 揭秘不思议地狱边境:全面攻略与生存指南
- 下一篇: 如何轻松开设股票账户
-
 掌握解二元一次方程的四大高效方法资讯攻略11-26
掌握解二元一次方程的四大高效方法资讯攻略11-26 -
 掌握一元二次方程公式法的轻松解题步骤资讯攻略01-05
掌握一元二次方程公式法的轻松解题步骤资讯攻略01-05 -
 二元一次方程的求解方法资讯攻略12-05
二元一次方程的求解方法资讯攻略12-05 -
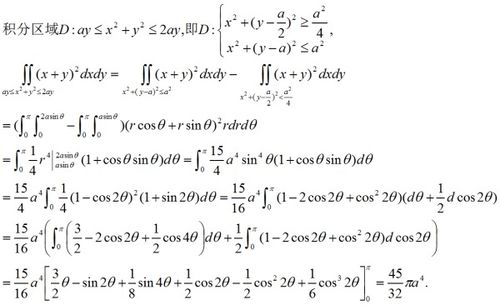 掌握二重积分dxdy的计算方法,轻松解题无烦恼资讯攻略10-24
掌握二重积分dxdy的计算方法,轻松解题无烦恼资讯攻略10-24 -
 高等数学入门:你了解全微分方程的概念及其解法吗?资讯攻略02-27
高等数学入门:你了解全微分方程的概念及其解法吗?资讯攻略02-27 -
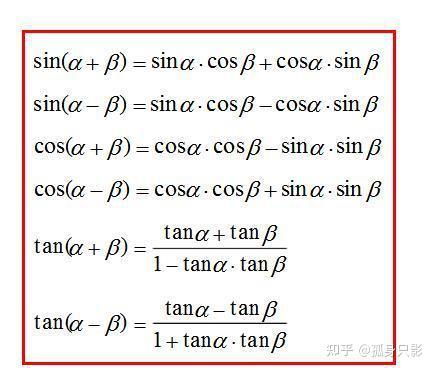 掌握三角函数公式,轻松解题无压力!资讯攻略11-28
掌握三角函数公式,轻松解题无压力!资讯攻略11-28