掌握一元二次方程公式法的轻松解题步骤
一元二次方程是数学中非常重要的一个概念,无论是在初中数学的学习中,还是在高中甚至更高级的数学课程中,都会频繁遇到。掌握一元二次方程的解法,尤其是公式法,对于解决复杂问题具有关键作用。下面,我们就来详细探讨一下一元二次方程公式法的具体步骤。

首先,我们需要明确一元二次方程的标准形式:ax²+bx+c=0,其中a、b、c是实数,并且a不等于0。公式法,就是通过特定的公式来求解这个方程。这个公式也被称为“求根公式”或“韦达定理”。

公式法的核心在于利用方程的系数a、b、c,通过一个公式直接计算出方程的解。这个公式是:

x=(-b±√(b²-4ac))/2a

这个公式看起来很复杂,但实际上它是有规律的,我们可以分步骤地来理解和应用它。
第一步:确认方程的形式
首先,确保你面对的是一个一元二次方程,并且它已经被整理为标准形式ax²+bx+c=0。如果方程不是这种形式,你可能需要先进行一些代数变换,比如合并同类项、移项等,来得到标准形式。
第二步:识别方程的系数
在确认方程为标准形式后,找出方程的系数a、b、c。这些系数是你在应用求根公式时需要输入的。
第三步:计算判别式
判别式Δ(Delta)是公式法中的一个关键部分,它决定了方程的根的类型。判别式的计算公式是:
Δ=b²-4ac
计算判别式的值,并根据这个值来判断方程的根的情况:
如果Δ>0,方程有两个不相等的实数根。
如果Δ=0,方程有两个相等的实数根,或者说有一个二重根。
如果Δ<0,方程没有实数根,但有两个共轭复数根。
第四步:应用求根公式
在计算出判别式后,就可以应用求根公式来求解方程的根了。求根公式是:
x=(-b±√(Δ))/2a
这里需要注意的是,由于判别式Δ可能是一个正数、零或负数,所以方程可能有两个实数根、一个二重实数根或两个复数根。当Δ是正数时,你需要计算两个根,分别对应于公式中的正负号;当Δ是零时,两个根相同,只需计算一次;当Δ是负数时,方程没有实数根,但你可以通过计算得到两个共轭复数根。
第五步:检查并解释解
在计算出方程的根后,需要检查你的计算是否正确。这可以通过将求得的根代回原方程来验证。如果计算正确,代入后的等式应该成立。
此外,还需要对解进行解释。这包括理解解的类型(实数根或复数根)、解的数量(一个或两个)以及解的具体值。在实际应用中,解的类型和数量往往比解的具体值更重要,因为它们可以告诉你关于方程所描述的系统的信息。
第六步:处理特殊情况
在使用公式法时,还需要注意一些特殊情况。比如,当a=0时,方程就不再是一元二次方程,而变成了一元一次方程。这时,你应该使用一元一次方程的解法来求解。另外,当b=0时,虽然方程仍然是一元二次方程,但求根公式中的-b项会消失,这可能会简化计算过程。然而,即使b=0,你仍然需要计算判别式并应用求根公式来确保得到正确的解。
另外,还有一些特殊情况需要注意。比如,当方程的系数是分数时,为了避免在计算过程中引入额外的误差,最好先将方程两边都乘以分母的最小公倍数,将系数化为整数。同样地,如果方程的系数非常大或非常小,可能需要使用科学记数法来表示它们,以便更准确地进行计算。
第七步:实践与应用
最后,要想真正掌握一元二次方程的公式法,大量的实践是必不可少的。通过解决各种类型的一元二次方程问题,你可以更加熟悉公式法的步骤和技巧,并培养自己的解题能力。
在实践中,你可能会遇到一些复杂的问题,比如需要解多个相关的一元二次方程、或者需要利用一元二次方程的解来求解其他问题(如最大值、最小值问题等)。这些问题可能会要求你更加灵活地应用公式法和其他数学技巧。
此外,一元二次方程在现实生活中的应用也非常广泛。比如,在物理学中,它们可以用来描述物体的运动轨迹;在经济学中,它们可以用来预测市场的变化趋势;在工程学中,它们可以用来计算结构的稳定性等。因此,通过实践和应用,你不仅可以提高自己的数学技能,还可以更好地理解这些方程在现实世界中的意义和价值。
总之,一元二次方程的公式法是一种强大而灵活的解题工具。通过理解和掌握这个方法的步骤和技巧,你可以更加有效地解决各种类型的一元二次方程问题,并培养自己的数学思维和解题能力。无论是在学习、工作还是生活中,这个技能都会给你带来很大的帮助和便利。
- 上一篇: 阿玛尼满天星手表真伪鉴别技巧大揭秘
- 下一篇: 精选好书推荐
-
 如何轻松掌握二元一次方程的解题步骤?资讯攻略12-05
如何轻松掌握二元一次方程的解题步骤?资讯攻略12-05 -
 掌握解二元一次方程的四大高效方法资讯攻略11-26
掌握解二元一次方程的四大高效方法资讯攻略11-26 -
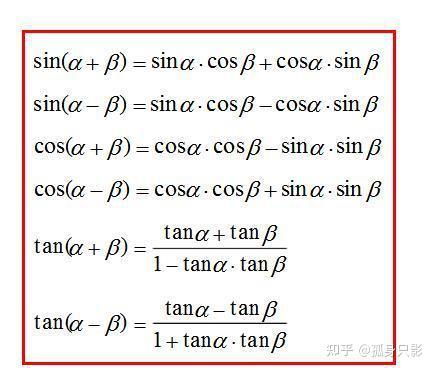 掌握三角函数公式,轻松解题无压力!资讯攻略11-28
掌握三角函数公式,轻松解题无压力!资讯攻略11-28 -
 掌握对数运算的核心公式,轻松解题无烦恼资讯攻略10-27
掌握对数运算的核心公式,轻松解题无烦恼资讯攻略10-27 -
 求解方程的六个关键公式资讯攻略11-09
求解方程的六个关键公式资讯攻略11-09 -
 如何求解一元二次方程的四种方法是什么?资讯攻略11-09
如何求解一元二次方程的四种方法是什么?资讯攻略11-09