探秘排列组合的神奇公式
排列组合是数学中一个非常基础且重要的概念,广泛应用于统计学、计算机科学、概率论以及日常生活等多个领域。它研究的是如何将一定数量的对象按照一定的顺序或无序的方式进行排列或组合。在深入探讨排列组合的公式之前,我们先来了解几个核心概念。
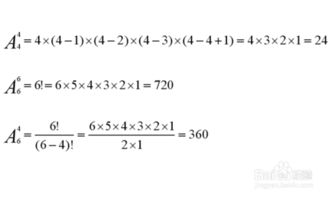
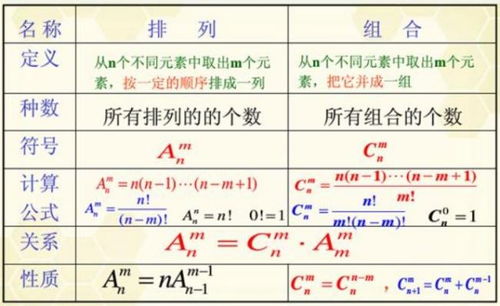
排列(Permutation)是指从n个不同元素中取出m(m≤n)个元素按照一定的顺序排成一列。这里的“顺序”意味着每一个排列都是独一无二的。例如,从集合{A, B, C}中取出两个元素的排列有:AB、AC、BA、BC、CA、CB,共6种。当我们考虑所有可能的排列时,使用的是排列公式。排列公式为:P(n,m) = n! / (n-m)!,其中“!”表示阶乘,即一个正整数的阶乘是所有小于及等于该数的正整数的积,0的阶乘为1。比如,5! = 5 × 4 × 3 × 2 × 1 = 120。

组合(Combination)则是指从n个不同元素中取出m(m≤n)个元素的所有取法。与排列不同的是,组合不考虑元素的顺序。也就是说,{A, B}和{B, A}在组合中视为同一种情况。组合的公式为:C(n,m) = n! / [m!(n-m)!]。组合数也被称为二项式系数,因为它与二项式定理(即(a+b)^n的展开式)中的系数有直接关系。例如,从集合{A, B, C}中取出两个元素的组合有:AB、AC、BC,共3种。

接下来,我们详细探讨几个常见的排列组合问题及其解法。
1. 不重复的排列
当我们需要从n个不同元素中取出m个元素进行排列,且每个元素只能使用一次时,我们称之为不重复的排列。这类问题直接使用上述的排列公式P(n,m)即可解决。例如,有4个人(A、B、C、D)参加一个比赛的决赛,我们需要确定他们获得前四名的所有可能顺序。这里n=4,m=4,所以排列数为P(4,4) = 4! / (4-4)! = 4! = 24种不同的排列方式。
2. 可重复的排列
与不重复的排列不同,可重复的排列允许某些元素被重复使用。例如,用数字0、1、2组成三位数,这里每个数字可以重复使用。为了计算这样的排列数,我们需要将每个位置看作独立的,因此总的排列数为3^3=27(因为每个位置都有3种选择)。对于一般情况,如果要从n种不同的元素中取出m个元素进行可重复的排列,那么排列数为n^m。
3. 不重复的组合
不重复的组合问题,即上述的组合公式C(n,m)的应用场景。它解决的是从n个不同元素中选出m个元素,不考虑顺序的所有可能取法。例如,从5个不同颜色的球中选出3个进行组合,组合数为C(5,3) = 5! / [3!(5-3)!] = 10种。
4. 分配问题
分配问题是一类特殊的排列组合问题,通常涉及将物品或任务分配给不同的人或组。例如,有6本不同的书分给甲、乙、丙三人,每人得到两本。这类问题可以通过分步乘法原理和组合公式结合来解决。首先,从6本书中选2本给甲,方法数为C(6,2);然后从剩下的4本书中选2本给乙,方法数为C(4,2);最后,丙得到剩下的2本。因此,总的分配方式为C(6,2) × C(4,2) × C(2,2) = 90种。
5. 排列组合中的相邻与不相邻问题
在某些排列组合问题中,需要考虑元素之间的相邻或不相邻关系。例如,有5个人站成一排,甲和乙必须相邻,求有多少种站法。解决这类问题,通常先将相邻的元素看作一个整体,然后再与其他元素一起进行排列。在这个例子中,先将甲和乙看作一个“大元素”,然后与其他3人一起进行4个“大元素”的排列,方法数为P(4,4)。而甲和乙两人之间又有P(2,2)种排列方式,所以总的排列数为P(4,4) × P(2,2) = 48种。
6. 环形排列
环形排列是指n个元素在圆上的一种排列方式。由于圆形排列具有旋转对称性,即旋转后的排列与原排列视为同一种情况,因此环形排列的公式为(n-1)!。例如,4个人围坐在圆桌旁,有(4-1)! = 6种不同的坐法。
7. 组合中的可重复问题
在某些组合问题中,允许某些元素被重复选择。例如,从{A, B, C}中选出2个元素(允许重复),有多少种组合?这类问题可以通过列举法或者考虑每个元素被选中的次数来解决。对于上述例子,组合有:AA、AB、AC、BB、BC、CC,共6种。
排列组合公式及其相关问题不仅在数学理论中占有重要地位,更是解决实际问题的重要工具。无论是在科学研究、工程设计还是日常生活中,我们都能见到排列组合的身影。掌握这些基本的排列组合公式和解题技巧,对于提高逻辑思维能力和解决问题的能力都大有裨益。通过不断练习和应用,我们可以更加灵活和高效地解决各种排列组合问题。
- 上一篇: 掌握Chrome地址栏的高效使用方法
- 下一篇: 笼盖四野的奇妙之旅
-
 CNM排列组合:揭秘高效计算的神奇公式!资讯攻略02-09
CNM排列组合:揭秘高效计算的神奇公式!资讯攻略02-09 -
 排列与组合:详解定义及实用公式资讯攻略11-03
排列与组合:详解定义及实用公式资讯攻略11-03 -
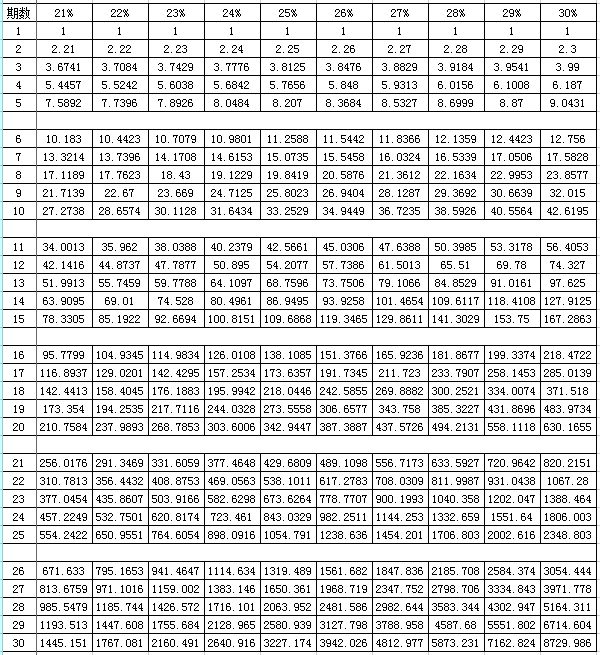 揭秘年金计算的神奇公式,轻松掌握未来财富密码!资讯攻略02-03
揭秘年金计算的神奇公式,轻松掌握未来财富密码!资讯攻略02-03 -
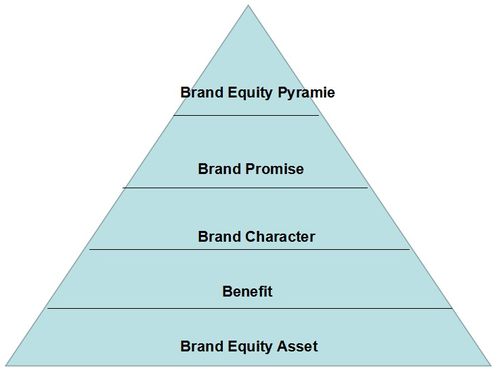 揭秘金字塔模型的神奇公式资讯攻略02-15
揭秘金字塔模型的神奇公式资讯攻略02-15 -
 揭秘长方体表面积的神奇计算公式!资讯攻略12-07
揭秘长方体表面积的神奇计算公式!资讯攻略12-07 -
 北京至张家口自驾游必去:探秘神奇天漠资讯攻略01-20
北京至张家口自驾游必去:探秘神奇天漠资讯攻略01-20












