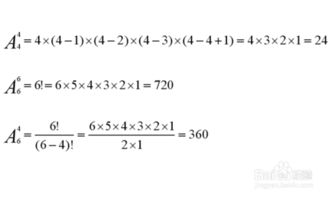排列与组合:详解定义及实用公式
在数学领域中,排列与组合是两个重要的概念,广泛应用于统计学、计算机科学、概率论等多个学科。理解这两个概念及其相关公式,对于解决实际问题具有重要意义。本文将详细介绍排列与组合的定义和公式,并辅以实例说明,以帮助读者更好地掌握这些基本概念。

排列与组合都涉及到从一组元素中选择一部分元素来形成新的集合或序列,但它们的区别在于是否考虑元素的顺序。排列是指从给定个数的元素中取出指定个数的元素进行排序,即需要考虑元素的顺序;而组合则是指从给定个数的元素中仅仅取出指定个数的元素,不考虑顺序。

排列的定义与公式
排列问题主要关注元素的顺序。假设有n个不同的元素,从中取出m(m≤n)个元素进行排列,那么这些排列的总数称为n个元素中取m个元素的排列数,记作P(n,m)或nPm。排列数的计算公式如下:

P(n,m) = n! / (n-m)!
其中,“!”表示阶乘运算,n! = n × (n-1) × ... × 2 × 1。
举例来说,如果有4个人(A、B、C、D)排队买票,那么有多少种不同的排队方式?这就是一个排列问题。从4个人中选出4个人进行排列,所以排列数为P(4,4) = 4! / (4-4)! = 4! = 24种不同的排队方式。
组合的定义与公式
组合问题则不关注元素的顺序,只关注元素的选择。假设有n个不同的元素,从中取出m(m≤n)个元素进行组合,那么这些组合的总数称为n个元素中取m个元素的组合数,记作C(n,m)或nCm。组合数的计算公式如下:
C(n,m) = n! / [m!(n-m)!]
这个公式可以通过排列数的公式推导出来。由于组合不考虑顺序,所以n个元素中取m个元素的排列数P(n,m)要除以m个元素的排列数P(m,m),即C(n,m) = P(n,m) / P(m,m) = [n! / (n-m)!] / [m! / 0!] = n! / [m!(n-m)!]。注意,0! = 1,这是阶乘运算的一个特殊规定。
以选择为例,如果有4种水果(苹果、香蕉、橘子、梨),想要从中选出2种水果作为午餐后的甜点,那么有多少种不同的选择方式?这就是一个组合问题。从4种水果中选出2种水果的组合数为C(4,2) = 4! / [2!(4-2)!] = 6种不同的选择方式。
排列与组合的关系与区别
排列与组合都涉及到从一组元素中选择部分元素,但关键在于是否考虑元素的顺序。排列需要考虑顺序,而组合则不需要。因此,对于同一个问题,如果考虑顺序,则用排列公式;如果不考虑顺序,则用组合公式。
从数学公式上也可以看出排列与组合的关系。排列数P(n,m)是组合数C(n,m)与m的阶乘的乘积,即P(n,m) = C(n,m) × P(m,m) = C(n,m) × m!。这反映了在考虑顺序的情况下,每一种组合都可以对应m!种不同的排列。
应用实例
排列与组合在实际生活中有广泛的应用。以下是一些具体的例子:
1. 密码设置:假设一个密码由4位数字组成,每一位数字可以是0-9中的任意一个,那么一共有多少种不同的密码?这是一个排列问题,因为每一位数字的顺序都很重要。所以,密码的总数为P(10,4) = 10! / (10-4)! = 5040种。
2. 球队阵容:一支足球队有11名球员,教练需要从这11名球员中选择5名球员作为首发阵容,那么有多少种不同的首发阵容?这是一个组合问题,因为首发阵容中的球员顺序并不重要。所以,首发阵容的总数为C(11,5) = 11! / [5!(11-5)!] = 462种。
3. 彩票中奖:假设一个彩票有6个数字位,每一位数字可以是0-9中的任意一个,且顺序很重要(即012345和543210是两种不同的中奖号码),那么一注彩票中奖的概率是多少?这同样是一个排列问题。首先,所有可能的彩票组合数为P(10,6) = 10! / (
- 上一篇: 揭秘:萤火虫闪烁光芒的神奇奥秘
- 下一篇: 农村医保网上缴费指南:轻松几步完成支付
-
 CNM排列组合:揭秘高效计算的神奇公式!资讯攻略02-09
CNM排列组合:揭秘高效计算的神奇公式!资讯攻略02-09 -
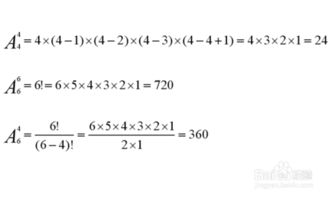 探秘排列组合的神奇公式资讯攻略11-26
探秘排列组合的神奇公式资讯攻略11-26 -
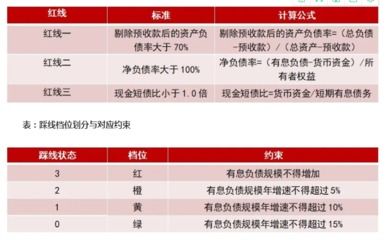 轻松掌握:资产负债率计算公式详解资讯攻略11-13
轻松掌握:资产负债率计算公式详解资讯攻略11-13 -
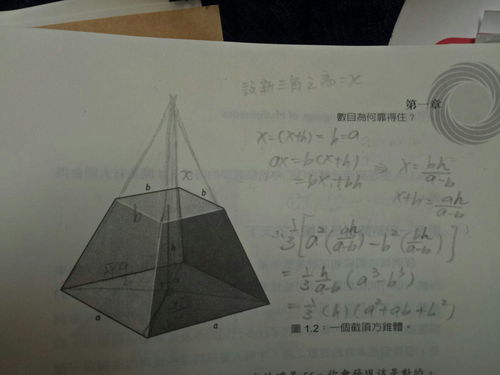 棱锥体积公式详解,轻松掌握!资讯攻略10-30
棱锥体积公式详解,轻松掌握!资讯攻略10-30 -
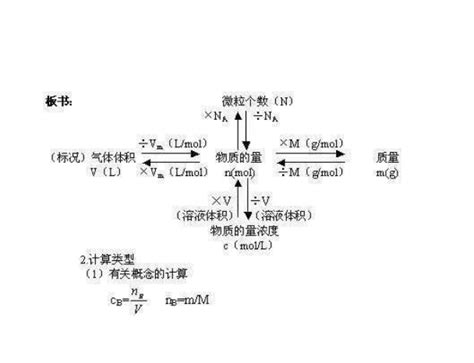 气体摩尔体积的定义及公式资讯攻略11-03
气体摩尔体积的定义及公式资讯攻略11-03 -
 揭秘:电流计算公式详解资讯攻略11-04
揭秘:电流计算公式详解资讯攻略11-04