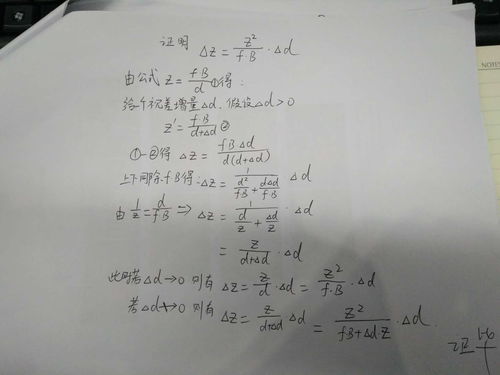掌握现值、终值与年金计算的6大核心公式
现值终值年金在金融学和财务管理中占据着核心地位,它们是评估投资项目、贷款还款和养老金计划等财务决策的重要工具。本文将详细介绍现值终值年金的六个基本公式,帮助读者更好地理解和应用这些概念。

复利终值公式
复利终值公式用于计算未来某一时点的本利和,它考虑了利息的多次计算。公式为:

\[ FV = P \times (F/P, i, n) \]

或者更详细地表示为:

\[ FV = P \times (1 + i)^n \]
其中:
\( FV \) 是未来价值(Future Value)。
\( P \) 是本金(Present Value)。
\( i \) 是每期的利率(Interest Rate)。
\( n \) 是期数(Number of Periods)。
\((F/P, i, n)\) 是复利终值系数,可通过查表或使用计算器得到。
这个公式可以帮助我们确定在给定利率和期数下,本金在未来某一时刻的累积值。
复利现值公式
复利现值公式用于计算现在需要投入的本金,以便在未来某一时点达到特定的本利和。公式为:
\[ P = FV \times (P/F, i, n) \]
或者更详细地表示为:
\[ P = FV \times (1 + i)^{-n} \]
其中:
\( P \) 是现值(Present Value)。
\( FV \) 是未来价值(Future Value)。
\( i \) 是每期的利率(Interest Rate)。
\( n \) 是期数(Number of Periods)。
\((P/F, i, n)\) 是复利现值系数,同样可通过查表或使用计算器得到。
这个公式有助于评估一项未来收入的当前价值,从而在财务决策中考虑资金的时间价值。
普通年金终值公式
普通年金终值公式用于计算一系列期末等额支付的年金在未来的总价值。公式为:
\[ FV = A \times (F/A, i, n) \]
或者更详细地表示为:
\[ FV = A \times \frac{(1 + i)^n - 1}{i} \]
其中:
\( FV \) 是年金终值(Future Value of Annuity)。
\( A \) 是每期支付的金额(Annuity Payment)。
\( i \) 是每期的利率(Interest Rate)。
\( n \) 是期数(Number of Periods)。
\((F/A, i, n)\) 是普通年金终值系数,可通过查表或使用计算器得到。
这个公式常用于计算固定金额的定期存款或养老金在未来某一时刻的总价值。
普通年金现值公式
普通年金现值公式用于计算一系列期末等额支付的年金现在的价值。公式为:
\[ P = A \times (P/A, i, n) \]
或者更详细地表示为:
\[ P = A \times \frac{1 - (1 + i)^{-n}}{i} \]
其中:
\( P \) 是年金现值(Present Value of Annuity)。
\( A \) 是每期支付的金额(Annuity Payment)。
\( i \) 是每期的利率(Interest Rate)。
\( n \) 是期数(Number of Periods)。
\((P/A, i, n)\) 是普通年金现值系数,可通过查表或使用计算器得到。
这个公式对于评估一系列未来支付(如贷款还款)的当前成本非常有用。
预付年金终值公式
预付年金终值公式用于计算一系列期初等额支付的年金在未来的总价值。由于预付年金在每期的期初支付,因此其终值会比普通年金更高。公式为:
\[ FV = A \times (F/A, i, n) \times (1 + i) \]
其中:
\( FV \) 是预付年金终值(Future Value of Prepaid Annuity)。
\( A \) 是每期支付的金额(Annuity Payment)。
\( i \) 是每期的利率(Interest Rate)。
\( n \) 是期数(Number of Periods)。
\((F/A, i, n)\) 是普通年金终值系数。
由于预付年金每期支付都在期初,所以在计算时需要将普通年金终值乘以 \((1 + i)\) 以反映更高的终值。
预付年金现值公式
预付年金现值公式用于计算一系列期初等额支付的年金现在的价值。同样地,由于预付年金在每期的期初支付,其现值也会与普通年金有所不同。公式为:
\[ P = A \times (P/A, i, n) \times (1 + i) \]
然而,这种表示方法通常是为了说明预付年金与普通年金之间的关系。实际上,预付年金现值更常见的计算公式是直接基于现值定义得出的:
\[ P = A \times \left[ \frac{1 - (1 + i)^{-(n+1)}}{i} \right] \]
或者通过查表得到预付年金现值系数,然后计算:
\[ P = A \times (P/A_{prepaid}, i, n) \]
其中:
\( P \) 是预付年金现值(Present Value of Prepaid Annuity)。
\( A \) 是每期支付的金额(Annuity Payment)。
\( i \) 是每期的利率(Interest Rate)。
\( n \) 是期数(Number of Periods)。
\((P/A_{prepaid}, i, n)\) 是预付年金现值系数,它通常是通过特殊公式或查表得到的。
递延年金现值公式
递延年金现值公式用于计算在一定延长期后才开始支付的年金现在的价值。公式有两种等价形式:
1. \( P = A \times (P/A, i, n) \times (P/F, i, m) \)
2. \( P = A \times [(P/A, i, m+n) - (P/A, i, m)] \)
其中:
\( P \) 是递延年金现值(Present Value of Deferred Annuity)。
\( A \) 是每期支付的金额(Annuity Payment)。
\( i \) 是每期的利率(Interest Rate)。
\( n \) 是连续收支期数(Number of Payment Periods)。
\( m \) 是递延期数(Number of Deferred Periods)。
\((P/A, i, n)\) 是普通年金现值系数。
\((P/F, i, m)\) 是复利现值系数,用于将未来支付折现到当前时间点。
这两个公式都可以用来计算递延年金的现值,选择哪一个取决于哪个公式更方便进行计算或查表。
通过以上六个公式的介绍,我们可以看到现值、终值和年金在金融学和财务管理中的重要性。这些公式不仅能够帮助我们进行投资决策、贷款还款计划制定和养老金规划,还能让我们更好地理解资金的时间价值,从而在财务决策中做出更加明智的选择。
- 上一篇: 阿撒兹勒:揭秘其象征的深邃原罪之谜
- 下一篇: 适合糖尿病患者的水果选择
-
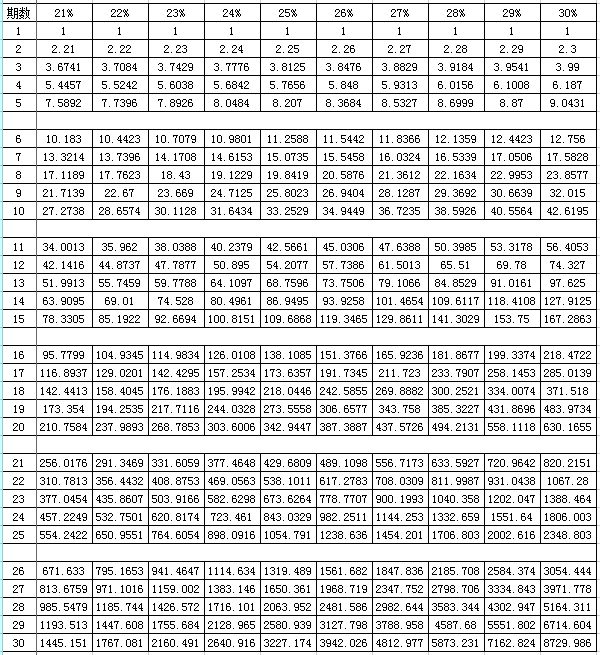 揭秘年金计算的神奇公式,轻松掌握未来财富密码!资讯攻略02-03
揭秘年金计算的神奇公式,轻松掌握未来财富密码!资讯攻略02-03 -
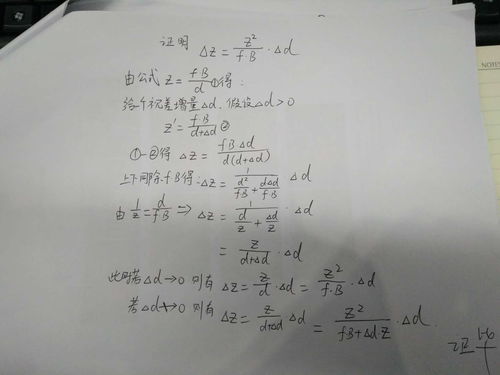 绝对误差与相对误差的计算公式详解资讯攻略12-06
绝对误差与相对误差的计算公式详解资讯攻略12-06 -
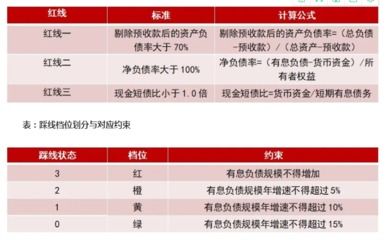 轻松掌握:资产负债率计算公式详解资讯攻略11-13
轻松掌握:资产负债率计算公式详解资讯攻略11-13 -
 卡西欧计算器计算方差的方法资讯攻略10-31
卡西欧计算器计算方差的方法资讯攻略10-31 -
 轻松掌握同比增长计算方法(附详细公式)资讯攻略10-28
轻松掌握同比增长计算方法(附详细公式)资讯攻略10-28 -
 掌握对数运算的核心公式,轻松解题无烦恼资讯攻略10-27
掌握对数运算的核心公式,轻松解题无烦恼资讯攻略10-27