绝对误差与相对误差的计算公式详解
在这个数据驱动的时代,每一个细微的数值差异都可能隐藏着巨大的信息价值。无论你是科研工作者、工程师、数据分析师,还是对学习充满热情的求知者,掌握“绝对误差”与“相对误差”的计算方法,都是提升数据精准度、优化决策过程的关键技能。今天,就让我们一起揭开这两个概念的神秘面纱,深入了解它们的计算公式,以及它们如何在各个领域发挥着不可替代的作用。
绝对误差:精准衡量偏差的基石
当我们谈论一个测量值与真实值之间的差异时,首先映入脑海的往往是“绝对误差”。顾名思义,绝对误差是指测量值(或计算值)与真值之间差的绝对值,它直接反映了测量或计算的准确程度。其计算公式简洁明了:绝对误差 = |测量值 - 真值|。这里的“| |”代表绝对值符号,意味着无论正负,我们只关心差异的大小。

为何绝对误差如此重要?

质量控制:在制造业中,产品尺寸的绝对误差直接影响到产品的合格与否,是质量控制的核心指标之一。
科学实验:在科研领域,精确测量是发现新规律、验证理论的前提。绝对误差帮助科学家判断实验数据的可靠性。
金融分析:在金融预测模型中,绝对误差小意味着预测更为准确,有助于减少投资风险。
相对误差:比例视角下的精度评估
如果说绝对误差是直观衡量误差大小的“尺子”,那么相对误差则是从比例的角度来审视误差,它揭示了误差相对于真值的占比。其计算公式为:相对误差 = |测量值 - 真值| / |真值| × 100%。这里的百分比形式使得相对误差在不同量级的数据之间具有可比性,是评估测量精度的一种更为灵活的方法。
相对误差的独到之处:
跨尺度比较:在处理具有不同数量级的数据时,相对误差提供了一个统一的评估标准,便于比较不同测量或计算结果的精度。
敏感性分析:在工程设计或模型优化中,相对误差能帮助识别哪些参数的变化对最终结果有显著影响,从而指导优化方向。
性能评估:在评估算法或模型的性能时,相对误差是衡量预测准确度的一个重要指标,特别是在处理非线性或复杂系统时。
实战演练:计算与理解
为了更好地理解绝对误差与相对误差,让我们通过一个简单的例子来实践它们的计算。
假设我们用某种仪器测量一个物体的长度,测量结果是10.5厘米,而经过高精度校准的标准测量结果是10厘米。那么:
绝对误差 = |10.5 - 10| = 0.5厘米
相对误差 = (0.5 / 10) × 100% = 5%
从这个例子中,我们可以看出,虽然绝对误差给出了误差的具体数值(0.5厘米),但相对误差(5%)更直观地告诉我们这个误差相对于真实尺寸的比例,这对于判断测量结果的可靠性尤为重要。
应用场景拓展:从日常到专业
日常生活:在烹饪时,按照食谱的配料比例,即使是小数点后几位的误差也可能影响最终的口感。这时,相对误差能帮助我们理解配料调整的合理性。
医疗诊断:在医学检测中,如血糖、血压等指标的测量,绝对误差和相对误差共同构成了医生评估病情的依据。
环境监测:在空气质量监测中,污染物的浓度变化往往以百分比的形式表达,相对误差是衡量监测设备准确性的关键指标。
航空航天:在航天器的设计中,任何微小的误差都可能导致任务失败。因此,绝对误差和相对误差的严格控制是确保飞行安全的基础。
精准之路:减少误差的策略
了解了绝对误差和相对误差之后,如何在实际操作中减少误差,提高数据的准确性呢?
1. 选用高精度仪器:选择具有更高精度的测量工具是减少误差的直接方法。
2. 多次测量取平均:通过多次重复测量并计算平均值,可以有效降低随机误差的影响。
3. 校准与验证:定期对测量设备进行校准,确保其处于最佳工作状态。同时,使用标准样品进行验证,确保测量结果的准确性。
4. 考虑环境因素:温度、湿度等环境因素可能影响测量结果,因此在测量时应尽量控制这些变量。
5. 数据分析方法:采用先进的数据分析方法,如误差分析、不确定性评估等,可以更深入地理解误差的来源和影响。
结语:迈向数据精准的新高度
在这个信息爆炸的时代,数据的准确性直接关系到决策的有效性和效率。掌握绝对误差和相对误差的计算方法,不仅能够提升我们处理和分析数据的能力,还能在多个领域推动科技创新和效率提升。无论是日常生活的小确幸,还是科学研究的大突破,都离不开对误差的精准把控。让我们携手踏上这段追求数据精准的旅程,共同探索未知,创造更加美好的未来。
- 上一篇: 轻松掌握抄手包制技巧
- 下一篇: 如何在Matlab中解方程?
-
 如何计算相对误差?资讯攻略11-04
如何计算相对误差?资讯攻略11-04 -
 圆周率的计算方法详解资讯攻略11-15
圆周率的计算方法详解资讯攻略11-15 -
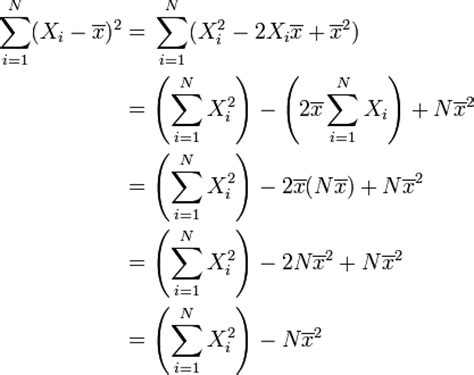 标准差公式是什么?资讯攻略10-29
标准差公式是什么?资讯攻略10-29 -
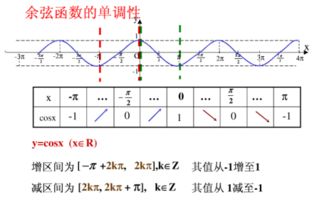 95%置信区间计算公式详解资讯攻略11-01
95%置信区间计算公式详解资讯攻略11-01 -
 揭秘:存贷比计算公式详解资讯攻略10-31
揭秘:存贷比计算公式详解资讯攻略10-31 -
 Excel中绝对值函数的优化使用公式资讯攻略11-03
Excel中绝对值函数的优化使用公式资讯攻略11-03