概率计算与统计分析方法
在我们日常生活中,概率和统计无处不在,它们帮助我们理解不确定性,做出明智的决策,并发现数据背后的规律。虽然这两个概念听起来有些复杂,但实际上,通过一些简单的例子和步骤,你就能轻松掌握如何计算概率和进行统计分析。

一、理解概率:生活中的可能性
概率是描述某一事件发生的可能性大小的数值。它的取值范围是从0到1,其中0表示事件不可能发生,1表示事件一定会发生。举个例子,抛一枚公平的硬币,正面朝上的概率就是0.5,因为有两种可能的结果(正面或反面),且每种结果出现的概率相等。

计算单一事件的概率
计算单一事件的概率公式为:
概率 = 事件发生的次数 ÷ 所有可能事件的次数
比如,从一副扑克牌(去掉大小王)中随机抽取一张,抽到红心的概率是:
概率 = 红心的牌数 ÷ 总牌数 = 13 ÷ 52 = 1/4
计算复合事件的概率
复合事件涉及两个或多个事件同时发生或相继发生的情况。这里介绍两种常见的复合概率类型:
1. 独立事件:一个事件的发生不影响另一个事件的发生。比如,连续抛两次硬币,每次正面朝上的概率都是0.5,两次都正面朝上的概率是0.5 × 0.5 = 0.25。
2. 互斥事件:两个事件不能同时发生。比如,从一副扑克牌中抽一张,这张牌要么是红心,要么不是红心,两者互斥。这种情况下,至少一个事件发生的概率是各自概率之和。
二、概率的实用应用:决策与风险
了解概率可以帮助我们做出更明智的决策,尤其是在面对不确定性和风险时。比如,在决定是否购买保险时,你可以考虑损失发生的概率以及损失的大小,来评估购买保险的必要性。
三、走进统计:数据的收集与分析
统计是对数据进行收集、整理、分析和解释的过程,它帮助我们从大量数据中提取有用的信息,理解数据的特征和趋势。
数据的收集
数据收集是统计分析的第一步,可以通过问卷调查、实验、观察、查阅记录等多种方式进行。关键是要确保数据的准确性和代表性,避免偏见和误差。
描述性统计:数据的初步探索
描述性统计用于总结和描述数据集的基本特征,主要包括:
集中趋势:平均数、中位数、众数等,用于描述数据的中心位置。
离散程度:方差、标准差、极差等,用于描述数据的分散程度。
分布形态:通过直方图、箱线图等图形展示数据的分布情况。
推断性统计:从样本到总体的推断
推断性统计是基于样本数据对总体参数进行估计和检验的方法。由于通常无法获取全部数据(总体),我们通过对样本的研究来推断总体的特性。
1. 参数估计:利用样本数据估计总体参数(如均值、比例)的值。例如,通过随机抽取一定数量的学生来估计全校学生的平均身高。
2. 假设检验:根据样本数据对关于总体的某个假设进行检验,判断其是否成立。常用的方法有t检验、卡方检验等。
四、实战演练:简单的概率与统计计算
例子1:抽奖活动的概率
某抽奖活动规定,从装有10个红球和5个蓝球的箱子中随机抽取一个球,如果抽到红球则中奖。计算中奖的概率。
解答:
总球数 = 红球数 + 蓝球数 = 10 + 5 = 15
中奖概率 = 红球数 ÷ 总球数 = 10 ÷ 15 = 2/3
例子2:考试成绩的分析
某班级30名学生的数学考试成绩如下(部分数据):85, 90, 78, 92, 88, 76, ...(假设数据已完整)。
计算平均分:将所有分数相加后除以人数。
计算标准差:先求每个分数与平均分的差的平方的平均值,再开方。
绘制直方图:将数据分组,统计每组内的数据个数,绘制成直方图以观察成绩的分布情况。
五、提升概率与统计能力的技巧
1. 多做练习:通过解决实际问题来加深理解,掌握计算技巧。
2. 阅读案例:阅读相关领域的案例,了解概率与统计在实际生活中的应用。
3. 使用工具:掌握Excel、SPSS、R等统计软件的使用,可以大大提高数据处理和分析的效率。
4. 关注新闻:很多新闻报道中都会涉及到统计数据和分析,关注这些新闻可以增强你对统计知识的敏感度。
六、结语
概率与统计是理解和分析世界的强大工具。通过掌握基本的概念和方法,我们不仅能够更好地应对日常生活中的不确定性,还能在科学研究、商业决策、健康管理等多个领域发挥重要作用。希望这篇文章能够帮助你开启概率与统计的学习之旅,享受数据带来的乐趣和洞见。
- 上一篇: 探索玩具新世界:益趣园里不可错过的7大精彩视频
- 下一篇: 揭秘:轻松查看已登录百度网盘的百度账号方法
-
 揭秘:抽样方法究竟包含哪几种?资讯攻略11-16
揭秘:抽样方法究竟包含哪几种?资讯攻略11-16 -
 数学中频率的计算方法或公式是什么资讯攻略11-19
数学中频率的计算方法或公式是什么资讯攻略11-19 -
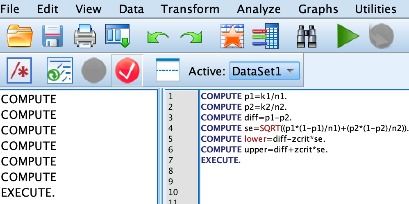 掌握计算总体率95%可信区间的简单方法资讯攻略11-01
掌握计算总体率95%可信区间的简单方法资讯攻略11-01 -
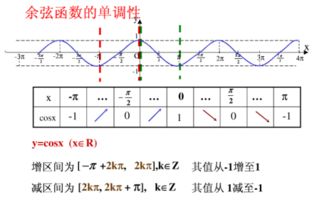 95%置信区间计算公式详解资讯攻略11-01
95%置信区间计算公式详解资讯攻略11-01 -
 如何计算C21资讯攻略12-07
如何计算C21资讯攻略12-07 -
 坐飞机发生坠机的概率有多大?资讯攻略10-30
坐飞机发生坠机的概率有多大?资讯攻略10-30












