掌握计算总体率95%可信区间的简单方法

如何计算总体率的95%可信区间

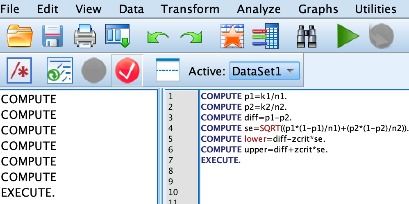
在统计学中，总体率（population proportion）是指某一事件在总体中发生的概率，通常用大写字母P表示。为了估计这一概率，我们会从总体中抽取一个样本，并计算样本率（sample proportion），用小写字母p表示。然而，样本率仅仅是总体率的一个估计值，其准确性受到样本大小、抽样方法等因素的影响。因此，我们需要计算总体率的置信区间，以表示我们对总体率估计的不确定性。

95%置信区间是最常用的置信区间之一，它表示我们有95%的信心认为总体率落在该区间内。计算总体率的95%置信区间有多种方法，其中较为常用的是正态近似法（Normal Approximation Method）和精确法（Exact Method）。以下是两种方法的详细步骤：

一、正态近似法

正态近似法适用于样本量较大（通常n*p>5且n*(1-p)>5）的情况。此时，样本率p的抽样分布近似于正态分布，可以利用正态分布的性质来计算置信区间。

1. 计算样本率p

首先，从总体中抽取一个样本，并计算样本率p。样本率p等于样本中事件发生的次数除以样本量n。

公式为：p = x/n

其中，x为样本中事件发生的次数，n为样本量。

2. 计算标准误SE

标准误（Standard Error, SE）是样本率p的抽样分布的标准差。标准误的计算公式为：

SE = sqrt(p*(1-p)/n)

其中，p为样本率，n为样本量。

3. 计算Z值

在95%置信水平下，Z值为1.96（这是标准正态分布下，两侧各2.5%的面积所对应的Z值）。

4. 计算置信区间

利用Z值和标准误SE，可以计算出总体率的95%置信区间。置信区间的下限和上限分别为：

下限 = p - Z*SE

上限 = p + Z*SE

将Z=1.96代入公式，得到：

下限 = p - 1.96*sqrt(p*(1-p)/n)

上限 = p + 1.96*sqrt(p*(1-p)/n)

二、精确法

精确法是基于二项分布的性质来计算置信区间的。对于小样本或样本率接近0或1的情况，正态近似法可能不够准确，此时应使用精确法。

1. 计算样本率p

与正态近似法相同，首先计算样本率p。

2. 确定置信水平

在95%置信水平下，我们有两个临界值，分别对应于二项分布累积分布函数的2.5%和97.5%分位点。

3. 计算临界值对应的样本量

利用二项分布的累积分布函数，找到使得置信区间上下限对应的概率分别为2.5%和97.5%的样本量（或称为成功次数）。这通常需要使用统计软件或查找二项分布表来完成。

4. 计算置信区间

根据找到的临界值对应的样本量（或成功次数），可以计算出置信区间的下限和上限。置信区间的下限是使得累积分布函数值为2.5%的最小样本率，上限是使得累积分布函数值为97.5%的最大样本率。

然而，由于二项分布的累积分布函数没有简单的解析式，因此精确法的计算通常依赖于统计软件或特定的表格。在实际应用中，可以使用如R语言、Python等统计软件中的相关函数来计算置信区间。

示例计算

假设我们从一个总体中抽取了一个样本量为100的样本，并发现其中有45个事件发生。我们可以使用上述方法来计算总体率的95%置信区间。

使用正态近似法：

1. 计算样本率p：p = 45/100 = 0.45

2. 计算标准误SE：SE = sqrt(0.45*(1-0.45)/100) = 0.0512

3. 使用Z值1.96计算置信区间：

下限 = 0.45 - 1.96*0.0512 = 0.3496

上限 = 0.45 + 1.96*0.0512 = 0.5504

因此，使用正态近似法得到的总体率的