线性代数:求解特征值与特征向量的方法
线性代数探秘:特征值与特征向量,究竟如何求解?

在线性代数的广袤天地里,特征值与特征向量无疑是最为璀璨夺目的星辰之一。它们不仅在理论研究中占据举足轻重的地位,更是工程、物理、计算机科学等多个领域解决实际问题不可或缺的工具。但你是否曾对这些神秘的概念感到困惑?那些复杂的公式和推导过程是否曾让你望而却步?别担心,今天,就让我们一起揭开特征值与特征向量的神秘面纱,看看它们究竟是如何求解的。

一、初识特征值与特征向量
在正式求解之前,我们首先要对特征值与特征向量有一个大致的了解。简单来说,特征值(Eigenvalue)和特征向量(Eigenvector)是方阵(Square Matrix)特有的属性。给定一个方阵A和一个非零向量v,如果存在一个标量(Scalar)λ,使得Av=λv成立,那么λ就被称为A的一个特征值,而v则被称为对应于λ的特征向量。

换句话说,特征值和特征向量描述了一个方阵对某个向量的“特殊作用”。当方阵A作用于向量v时,它仅仅是改变了v的模长(或方向),但v的指向(即v与A的特征向量之间的夹角)并未发生改变。这种“特殊作用”在许多实际问题中都有着广泛的应用。

二、求解特征值与特征向量的方法
方法一:特征多项式法
这是求解特征值和特征向量最常用也最直观的方法。其基本步骤如下:

1. 构建特征多项式:给定一个n阶方阵A,我们可以写出它的特征多项式f(λ)=|A-λI|,其中I是n阶单位矩阵。这个多项式的根就是A的特征值。
2. 求解特征值:通过求解特征多项式f(λ)=0,我们可以得到A的所有特征值。这些特征值可能是实数,也可能是复数。
3. 求解特征向量:对于每一个特征值λ,我们可以将其代入方程组(A-λI)x=0,求解得到对应的特征向量x。注意,这里的x可能不是唯一的,因为特征向量x的任意非零倍数仍然是特征向量。
例如,考虑一个简单的2x2矩阵A=[[2,1],[1,2]]。我们可以写出它的特征多项式f(λ)=|(2-λ,1),(1,2-λ)|=(2-λ)²-1=λ²-4λ+3=0。求解这个二次方程,我们得到两个特征值λ₁=1和λ₂=3。然后,我们可以分别将这两个特征值代入方程组(A-λI)x=0,求解得到对应的特征向量。
方法二:数值方法
对于大型矩阵或特征多项式难以直接求解的情况,我们可以采用数值方法来求解特征值和特征向量。常见的数值方法包括幂法、QR算法等。这些方法通常利用迭代的方式逐步逼近真实的特征值和特征向量。
方法三:特殊矩阵的简化求解
对于一些特殊类型的矩阵(如对称矩阵、三角矩阵等),我们可以利用它们的性质来简化求解过程。例如,对于对称矩阵A,它的特征值一定是实数,且不同特征值对应的特征向量一定是正交的。这些性质可以大大简化求解过程。
三、特征值与特征向量的应用
特征值与特征向量之所以重要,是因为它们在许多实际问题中都有着广泛的应用。以下是一些常见的应用场景:
1. 物理振动分析:在物理学中,特征值和特征向量可以用来描述系统的振动模式。例如,在结构力学中,我们可以通过求解结构的特征值和特征向量来预测其在不同频率下的振动情况。
2. 量子力学:在量子力学中,特征值和特征向量用来描述粒子的能量状态和波函数。这些状态是量子系统的基础属性,对于理解粒子的行为至关重要。
3. 图像处理:在计算机视觉和图像处理领域,特征值和特征向量可以用来进行图像压缩、边缘检测等任务。通过提取图像的特征值和特征向量,我们可以有效地降低图像的维度,同时保留图像的重要信息。
4. 机器学习:在机器学习中,特征值和特征向量也被广泛用于降维、聚类、分类等任务。例如,在主成分分析(PCA)中,我们通过求解数据矩阵的特征值和特征向量来找到数据的主要成分,从而实现降维的目的。
四、结语
特征值与特征向量作为线性代数的核心内容之一,其重要性不言而喻。通过求解特征值和特征向量,我们可以深入了解矩阵的性质和行为,为解决实际问题提供有力的数学工具。虽然求解过程可能涉及复杂的计算和推导,但只要我们掌握了基本的方法和技巧,就能够轻松地应对各种挑战。
在探索线性代数的道路上,特征值与特征向量无疑是一个重要的里程碑。它们不仅揭示了矩阵的“内在”性质,更为我们打开了一扇通往未知世界的大门。无论你是数学爱好者、科研人员还是工程师,掌握
- 上一篇: 山东济宁市精品旅游景点全攻略
- 下一篇: 揭秘:潮湿的绝对反义词竟然是什么?
-
 揭秘:如何求解矩阵的特征向量?资讯攻略10-27
揭秘:如何求解矩阵的特征向量?资讯攻略10-27 -
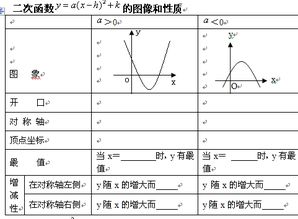 探索二次函数:图像之美与性质之谜资讯攻略11-08
探索二次函数:图像之美与性质之谜资讯攻略11-08 -
 如何在MATLAB中轻松求解各种方程?资讯攻略12-05
如何在MATLAB中轻松求解各种方程?资讯攻略12-05 -
 如何用Matlab解方程?资讯攻略01-13
如何用Matlab解方程?资讯攻略01-13 -
 如何求解轨迹方程的五种常用方法?资讯攻略12-01
如何求解轨迹方程的五种常用方法?资讯攻略12-01 -
 揭秘矩阵逆的求解奥秘资讯攻略11-04
揭秘矩阵逆的求解奥秘资讯攻略11-04












