如何在MATLAB中轻松求解各种方程？

在科学与工程的各个领域，数学方程是描述自然现象、预测系统行为以及优化设计的重要工具。MATLAB，作为一款强大的数学计算软件，提供了丰富的函数和工具箱，使得求解各种方程变得高效而直观。本文将围绕“怎么用MATLAB解方程”这一主题，详细介绍MATLAB在解线性方程组、非线性方程、微分方程以及方程组求解方面的应用。

一、解线性方程组

线性方程组是由一组线性方程组成的系统，其未知数个数与方程个数可能相等或不等。MATLAB提供了多种方法求解线性方程组，其中最基本的是使用反斜杠操作符（\）或`linsolve`函数。

示例：使用反斜杠操作符

假设有一个线性方程组Ax = b，其中A是系数矩阵，b是常数向量。我们可以直接利用MATLAB的命令窗口或脚本求解。

```matlab

A = [2, -1, 1; 3, 3, 9; 3, 3, 5];

b = [2; -1; 2];

x = A \ b;

disp(x);

```

上述代码将输出方程组Ax = b的解向量x。

示例：使用`linsolve`函数

对于符号变量组成的线性方程组，可以使用`linsolve`函数。

```matlab

syms x y z;

A = [2*x - y + z, -x + 2*y, x + y - z];

b = [2*x, -x, x];

sol = linsolve(A == b, [x, y, z]);

disp(sol);

```

此例中，我们定义了符号变量x、y、z，并求解了方程组A = b的解。

二、解非线性方程

非线性方程组的求解相比线性方程组更为复杂，MATLAB提供了`fsolve`函数来数值求解非线性方程组。

示例：使用`fsolve`函数

考虑一个非线性方程组：

\[

\begin{cases}

x_1^2 + x_2^2 = 4 \\

(x_1 - 1)^2 + x_2^2 = 1

\end{cases}

\]

我们可以编写一个函数来定义方程组，并使用`fsolve`求解。

```matlab

function F = nonlin_eqs(x)

F(1) = x(1)^2 + x(2)^2 - 4;

F(2) = (x(1) - 1)^2 + x(2)^2 - 1;

end

% 初始猜测值

x0 = [2; 0];

% 求解非线性方程组

sol = fsolve(@nonlin_eqs, x0);

disp(sol);

```

三、解微分方程

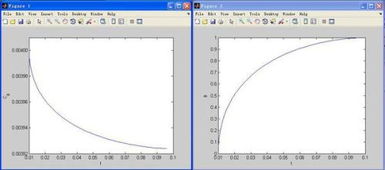
微分方程是描述变量随时间或其他变量变化规律的数学工具。MATLAB中的`ode`系列函数（如`ode45`、`ode23`等）可用于求解常微分方程（ODEs）。

示例：使用`ode45`求解一阶和二阶微分方程

考虑一个简单的一阶微分方程：

\[

\frac{dy}{dt} = -2y

\]

以及一个二阶微分方程：

\[

\frac{d^2y}{dt^2} - y = 0

\]

我们可以分别定义这两个方程，并使用`ode45`求解。

```matlab

% 一阶微分方程

dydt = @(t, y) -2*y;

[t1, y1] = ode45(dydt, [0 5], 1); % 初始条件y(0) = 1

plot(t1, y1);

xlabel('Time t');

ylabel('y(t)');

title('Solution of First Order ODE');

% 二阶微分方程，转化为一阶方程组

function dydt = second_order_ode(t, y)

dydt = zeros(2,1);

dydt(1) = y(2); % dy1/dt = y2

dydt(2) = y(1); % dy2/dt = y1

end

% 初始条件

y0 = [1; 0]; % y(0) = 1, y'(0) = 0

[t2, y2] = ode45(@second_order_ode, [0 10], y0);

plot(t2, y2(:,1));

xlabel('Time t');

ylabel('y(t)');

title('Solution of Second Order ODE');

```

四、方程组求解的高级技巧

在解决复杂方程组时，可能需要采用一些高级技巧，如使用符号计算工具箱进行精确求解、利用优化工具箱进行全局搜索、或者结合图形界面进行交互式求解。

符号计算工具箱

对于涉及符号变量的方程组，MATLAB的符号计算工具箱提供了强大的功能。例如，可以使用`solve`函数求解符号方程组。

```matlab

syms x y;

eq1 = x^2 + y^2 == 4;

eq2 = (x - 1)^2 + y^2 == 1;

[sol_x, sol_y] = solve(eq1, eq2, [x, y]);

disp(sol_x);

disp(sol_y);

```

优化工具箱

对于非线性方程组，特别是当存在多个解或需要全局最优解时，可以利用MATLAB的优化工具箱进行求解。例如，`ga`函数（遗传算法）可用于全局搜索。

```matlab

% 定义目标函数（方程组误差的平方和）

fun = @(x) sum(([x(1)^2 + x(2)^2 - 4; (x(1) - 1)^2 + x(2)^2 - 1]).^2);

% 初始种群

x0 = rand(2,100); % 100个初始解

% 遗传算法求解

[x, fval] = ga(fun, 2); % 2个变量

disp(x); % 解

disp(fval); % 目标函数值（误差平方和）

```

结语

MATLAB作为一款功能强大的数学计算软件，为科学计算和工程应用提供了丰富的工具。通过本文的介绍，读者可以了解到如何使用MATLAB求解线性方程组、非线性方程、微分方程以及方程组的高级求解技巧。无论是数值计算还是符号计算，MATLAB都能提供高效、准确的解决方案，是科研人员和工程师不可或缺的工具之一。