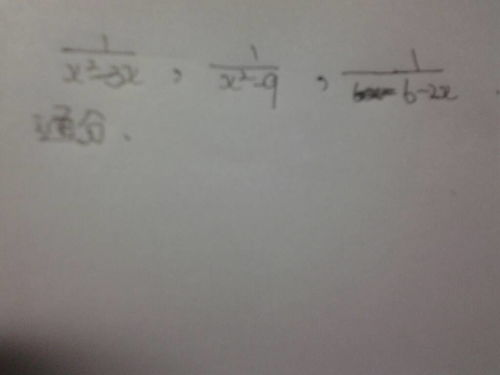如何找到分式的最简公分母？

在数学的广阔天地里，分式是一个既常见又重要的概念。它像是一个小小的魔法棒，能让我们在数的世界里进行各种奇妙的变换。然而，对于初学者来说，分式有时候也会带来一些困惑，尤其是当我们需要找到分式的最简公分母时。别担心，今天我们就来一起揭开这个谜团，用通俗易懂的语言，详细讲解如何找到分式的最简公分母。

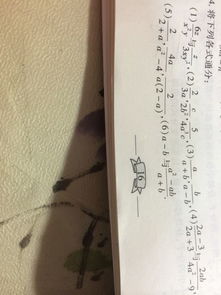
首先，我们要明白什么是公分母。简单来说，当我们有两个或更多的分式需要相加、相减时，为了能让它们“站在同一起跑线上”，我们需要找到一个共同的分母，这个共同的分母就是公分母。而最简公分母，则是这个公分母中最简单、最不可约分的形式。

那么，如何找到这个最简公分母呢？我们可以分三步走：

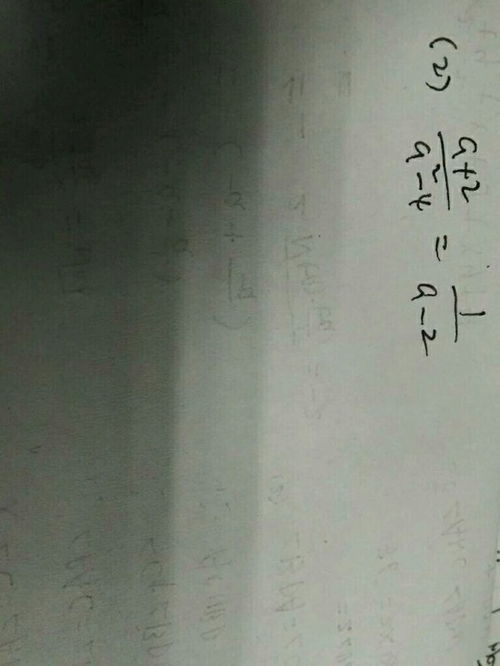
第一步：分解质因数

这一步是找到最简公分母的基础。我们需要将每个分式的分母都分解成质因数。质因数，就是只能被1和它本身整除的数，比如2、3、5、7等。分解质因数的方法很简单，就是不断地用最小的质数去除这个数，直到除到1为止。

比如，我们有两个分式，它们的分母分别是6和10。我们可以这样分解它们的质因数：

6 = 2 × 3

10 = 2 × 5

第二步：取各质因数的最高次幂

在分解完质因数之后，我们需要看看每个质因数在各个分母中出现的最高次幂是多少。为什么要这么做呢？因为我们要找的是最简公分母，而最简公分母需要包含所有分母中出现的质因数，并且每个质因数的次数都要取最高的那个。

还是以上面的6和10为例。在6的质因数分解中，2和3都出现了1次；在10的质因数分解中，2出现了1次，5也出现了1次。所以，我们取2和3的最高次幂（都是1次），再取5的最高次幂（也是1次），然后将它们相乘，得到：

2^1 × 3^1 × 5^1 = 2 × 3 × 5 = 30

所以，6和10的最简公分母就是30。

第三步：组合成最简公分母

在找到了所有质因数的最高次幂之后，我们只需要将它们相乘，就可以得到最简公分母了。这一步其实很简单，就是做乘法运算而已。

当然，有时候我们可能会遇到一些特殊情况，比如分母中有小数或者带分数。这时候，我们需要先将它们转化为假分数（即分子和分母都是整数的分数），然后再按照上面的步骤来求解最简公分母。

另外，还有一些小技巧可以帮助我们更快地找到最简公分母：

1. 观察法：有时候，我们可以通过观察直接找到最简公分母。比如，当两个分母是相邻的整数时，它们的最简公分母就是这两个整数的乘积。

2. 倍数关系：如果两个分母之间存在倍数关系，那么它们的最简公分母就是较大的那个分母。比如，8和16的最简公分母就是16，因为16是8的2倍。

3. 公式法：对于一些特殊的分式（比如分母是多项式的情况），我们可以使用公式法来求解最简公分母。比如，对于两个分母都是二次多项式的分式，我们可以使用求根公式或者因式分解法来找到它们的最简公分母。

不过，需要注意的是，虽然这些方法可以帮助我们更快地找到最简公分母，但是在使用它们之前，我们还是要先确保自己理解了最简公分母的基本概念和方法。因为只有这样，我们才能在遇到复杂问题时，灵活运用这些方法来解决它们。

找到了最简公分母之后，我们就可以进行分式的加减运算了。具体的方法就是将每个分式的分子和分母都乘以一个适当的数（这个数就是使得原分母变为最简公分母的数），使得所有的分式都变为以最简公分母为分母的形式。然后，我们就可以像加减整数一样，对它们的分子进行加减运算了。

最后，需要提醒的是，虽然最简公分母在分式的加减运算中起着非常重要的作用，但是在实际的应用中，我们还需要注意一些其他的问题。比如，当分式的分子或分母含有字母时，我们需要先对它们进行因式分解，然后再找出最简公分母。另外，当分式的分母含有根号时，我们也需要先对它们进行有理化处理，然后再进行运算。

总的来说，找到分式的最简公分母并不是一件难事。只要我们理解了它的基本概念和方法，并且掌握了相关的技巧和小贴士，就可以轻松应对各种复杂的问题了。希望这篇文章能够帮助你更好地理解分式的最简公分母，并在实际的学习中取得更好的成绩！