分式概念详解

分式是两个整式相除的商式，其中分子为被除式，分母为除式，分式的分母中必须含有字母，分式的分子和分母都是代数式，且都是整式。分式可以表示具体的量，也可以表示两个量之间的关系。分式有意义的前提是分母不能为0。分式的基本性质是分式的分子和分母同时乘以（或除以）同一个不为0的整式，分式的值不变。约分是分式约分，把一个分数的分子、分母同时除以公因数，分数的值不变。这个变化过程叫做约分。通分是根据分数（式）的基本性质，把几个异分母的分式（或分数）化为与原来的分式（或分数）相等的同分母的分式（或分数）。约分和通分体现了数学中的转化思想。

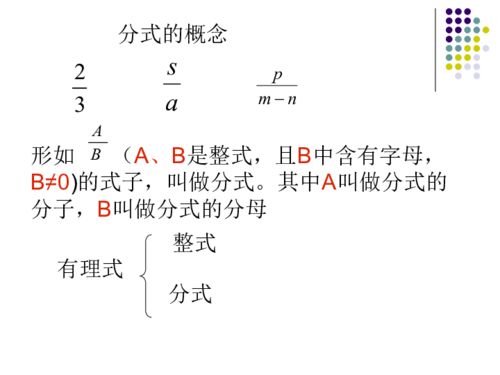
在分数中，分子与分母同时乘以（或除以）同一个不为0的整式，分数的大小不变。这叫做分式的基本性质。即分式的分子和分母乘（或除以）同一个不等于0的整式，分式的值不变。分式中的符号法则，分子、分母、分式本身任意改变两项的符号，分式的值不变。即若把分式的分子a与分母b同时改变符号，分式的值不变。分式的分子和分母同时乘以-1，分式的值不变。若分式的分子、分母都是几个因式的积，则约去分子、分母中相同的因式，分式的值不变。若分式的分子、分母中有多项式，则先进行因式分解，约去分子、分母中的公因式后，再约去分子、分母中相同的因式的幂。

分式的约分方法是，如果分式的分子和分母都是单项式或者是几个因式的乘积，那么可以直接将其公因式约去；如果分子和分母都是多项式，那么可以先将它们分别因式分解，然后约去公因式。注意在约分的过程中，公因式都要约尽。最简分式的标准是分子、分母中不含有公因式，即不能再约分。

分式的通分关键是确定最简公分母，其步骤如下：将各个分式的分母分解因式；找出各分母系数的最小公倍数；凡单独出现的字母连同它的指数作为最简公分母的一个因式；将上述取得的各因式相乘，得到最简公分母。然后进行通分，根据分式的基本性质，把几个异分母的分式，化成与原来的分式相等的同分母的分式，叫做分式的通分。通分的关键是确定几个分式的最简公分母，其步骤如下：将各个分式的分母分解因式；找出各分母系数的最小公倍数；凡单独出现的字母连同它的指数作为最简公分母的一个因式；将上述取得的各因式相乘，得到最简公分母。

对于分母不含有字母的分式，其通分的关键是求各分母的最小公倍数；对于分母是多项式时，首先要对多项式进行因式分解，然后再求最简公分母。通分和约分是互为逆运算的过程。在进行分式的约分和通分时，一定要注意“都”和“相同”的含义。对于分子和分母都是单项式，且没有公因式的分式，它的最简形式就是它本身。对于分子和分母都是多项式，要把其化为最简形式，首先要对分子和分母作因式分解，然后再化为最简形式。

分式的分子与分母同时乘（或除以）同一个不为0的整式，分式的值不变。这叫做分式的基本性质。其中，整式包括单项式和多项式。例如，如果有一个分式a/b，其中a和b都是整式，那么可以乘以一个不为0的整式c，得到(a*c)/(b*c)，这个新分式的值与原分式的值相同。同样地，也可以除以一个不为0的整式d，得到(a/d)/(b/d)，这个新分式的值也与原分式的值相同。这就是分式的基本性质的应用。

在进行分式的计算时，经常需要用到这个性质。例如，在分式的加减法中，如果两个分式的分母不同，那么就需要先通分，即将两个分式的分母化为相同的数，然后再进行加减运算。通分的过程就需要用到分式的基本性质，即分子分母同时乘以或除以同一个不为0的整式，分式的值不变。在分式的乘除法中，也需要用到分式的基本性质。例如，在进行分式的乘法运算时，如果两个分式的分子分母有相同的因式，那么就可以约去这个因式，使得运算更加简便。在进行分式的除法运算时，可以将除数取反变为乘法，然后再利用分式的基本性质进行化简。

分式在实际生活中也有着广泛的应用