质点是什么?如何判断一个物体能否视为质点?
在物理学中,质点是一个至关重要的概念,它简化并抽象了物体的运动,使得我们能够忽略物体的形状、大小、内部结构以及旋转等因素,专注于研究物体的位置和速度等运动状态。质点的引入,极大地简化了物理问题的复杂性,让我们能够更加深入地理解物体的运动规律。本文将从质点的定义、质点的判断方法以及质点概念的运用等多个维度,探讨质点在物理学中的重要性。

一、质点的定义

质点,简单来说,就是一个具有质量的几何点。这里的“几何点”意味着它没有形状、大小和内部结构,仅代表物体在空间中的位置。而“质量”则是物体惯性大小的度量,决定了物体在受到外力作用时运动状态改变的难易程度。因此,质点是物理学中为了简化问题而提出的理想化模型。
在实际应用中,当物体的形状、大小以及内部结构对研究的问题影响可以忽略不计时,我们就可以将该物体视为质点。例如,在研究地球绕太阳的公转时,地球的形状、大小以及内部结构对公转轨道的影响微乎其微,因此可以将地球视为一个质点。同样地,在研究子弹的飞行轨迹时,也可以忽略子弹的形状和大小,将其视为质点。

需要注意的是,质点并不是一个真实存在的物体,而是一个理想化的物理模型。它的引入是为了简化问题,让我们能够更加专注于研究物体的运动状态和运动规律。
二、质点的判断方法
判断一个物体是否可以视为质点,需要从多个维度进行综合考虑。以下是一些常用的判断方法:
1. 研究问题的性质
首先,要明确研究的问题是什么。如果研究的是物体的整体运动状态,如位置、速度、加速度等,并且物体的形状、大小以及内部结构对这些问题的影响可以忽略不计,那么就可以将物体视为质点。例如,在研究行星绕恒星的公转时,行星的形状、大小以及内部结构对公转轨道的影响很小,因此可以将行星视为质点。
2. 物体的形状和大小
其次,要考虑物体的形状和大小。如果物体的形状和大小与研究的问题相比非常小,那么就可以忽略其形状和大小,将其视为质点。例如,在研究原子核内部的粒子运动时,原子核的形状和大小与粒子间的距离相比非常小,因此可以将原子核视为质点。
3. 物体的内部结构
此外,还需要考虑物体的内部结构。如果物体的内部结构对研究的问题没有影响,或者影响可以忽略不计,那么就可以将物体视为质点。例如,在研究地球的公转时,地球的内部结构(如地壳、地幔、地核等)对公转轨道的影响很小,因此可以将地球视为质点。
4. 物体的运动状态
最后,还要考虑物体的运动状态。如果物体的运动状态是平动(即物体上各点的运动轨迹相同),那么就可以将物体视为质点。因为在平动中,物体的形状和大小对运动状态没有影响。例如,在研究火车在平直轨道上匀速行驶时,火车的形状和大小对行驶轨迹没有影响,因此可以将火车视为质点。
综上所述,判断一个物体是否可以视为质点需要从研究问题的性质、物体的形状和大小、物体的内部结构以及物体的运动状态等多个维度进行综合考虑。只有当这些条件都满足时,才能将物体视为质点进行简化处理。
三、质点概念的运用
质点概念的引入极大地简化了物理问题的复杂性,使得我们能够更加深入地理解物体的运动规律。以下是一些质点概念在物理学中的运用实例:
1. 牛顿运动定律
在牛顿运动定律中,质点是一个重要的研究对象。通过引入质点的概念,我们可以将复杂的物体运动问题简化为质点的运动问题。例如,在研究物体的自由落体运动时,可以将物体视为质点,忽略其形状和大小对运动状态的影响,从而得到简洁明了的运动方程。
2. 万有引力定律
在万有引力定律中,质点也是一个重要的概念。根据万有引力定律,任何两个物体之间都存在引力作用,且引力的大小与两物体的质量成正比,与两物体之间的距离的平方成反比。当研究两个天体之间的引力作用时,可以将它们视为质点,从而简化计算过程。例如,在研究地球绕太阳的公转时,可以将地球和太阳都视为质点,从而得到地球公转轨道的方程。
3. 动量定理和动能定理
在动量定理和动能定理中,质点也是一个重要的研究对象。通过引入质点的概念,我们可以将复杂的碰撞问题简化为质点的碰撞问题。例如,在研究两个小球之间的弹性碰撞时,可以将它们视为质点,忽略其形状和大小对碰撞过程的影响,从而得到简洁明了的碰撞方程。
4. 振动和波动
在振动和波动的研究中,质点也是一个重要的概念。通过引入质点的概念,我们可以将复杂的振动和波动问题简化为质点的振动和波动问题。例如,在研究简谐振动时,可以将振动体
- 上一篇: 轻松学会:手机如何快速连接电脑
- 下一篇: 如何轻松充值QQ里的Q币
-
 如何绘制最速曲线资讯攻略01-23
如何绘制最速曲线资讯攻略01-23 -
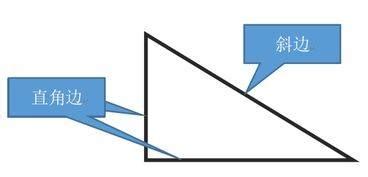 三条边能否构成三角形的判断方法是什么?资讯攻略02-20
三条边能否构成三角形的判断方法是什么?资讯攻略02-20 -
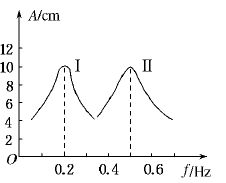 单摆的周期定义资讯攻略11-27
单摆的周期定义资讯攻略11-27 -
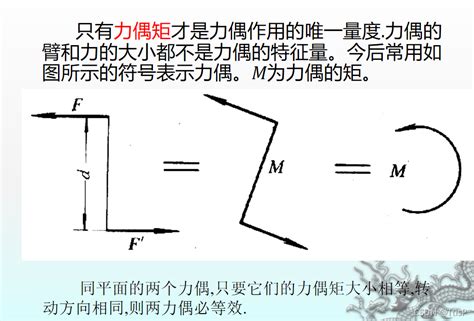 力偶矩顺时针判断技巧揭秘资讯攻略11-10
力偶矩顺时针判断技巧揭秘资讯攻略11-10 -
 不透露时,男性能否判断女性是否为处女?资讯攻略12-05
不透露时,男性能否判断女性是否为处女?资讯攻略12-05 -
 初一能否洗澡?了解这一日常习惯的特别之处资讯攻略03-18
初一能否洗澡?了解这一日常习惯的特别之处资讯攻略03-18











