圆柱与圆锥的关联解析
圆柱和圆锥那些不得不说的关系
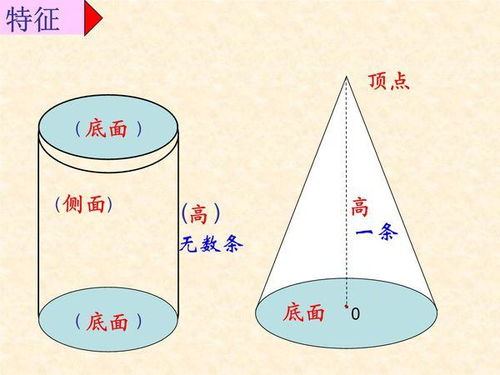
在几何学的世界里,圆柱和圆锥是两种既独特又紧密相关的立体图形。它们各自拥有独特的形状和性质,但同时又存在着一种微妙的内在联系,这种关系不仅在数学理论中占据重要地位,更在实际应用中展现出无穷的魅力和实用性。
首先,让我们来回顾一下圆柱和圆锥的基本定义。圆柱是一个由两个平行且相等的圆形底面以及连接这两个底面的侧面围成的立体图形。它的高是两个底面圆心之间的距离,底面半径则决定了圆柱的粗细。而圆锥则是由一个圆形底面和一个顶点不在底面平面上的侧面围成的立体图形,侧面展开后是一个扇形。圆锥的高是从顶点到底面圆心的距离,底面半径则决定了圆锥的大小。
尽管圆柱和圆锥在形状上看似迥异,但它们之间却存在着一种惊人的相似之处,即它们都可以通过旋转一个二维图形来生成。圆柱是由一个矩形绕其一边旋转而成,而圆锥则是由一个直角三角形绕其一直角边旋转而成。这种生成方式不仅揭示了圆柱和圆锥的几何本质,还为它们之间的进一步关系提供了线索。
接下来,我们深入探讨圆柱和圆锥之间的内在联系。一个最直观的发现是,当圆柱的高与底面半径相等时,我们可以将其侧面展开并重新卷绕,形成一个与底面半径相同的圆锥。这个圆锥的高也恰好等于原圆柱的高和底面半径。这个有趣的性质揭示了圆柱和圆锥在某种特定条件下的等价性,也为它们之间的转换提供了可能。
然而,这种等价性并非总是存在。在一般情况下,圆柱和圆锥的形状和尺寸都是独立的。但正是这种独立性,使得它们在实际应用中能够灵活地满足各种需求。例如,在建筑设计中,圆柱常被用作支撑结构,其稳定的形状和均匀的受力分布使得它成为理想的承重构件。而圆锥则因其独特的形状和流线型设计,常被用于屋顶、灯塔等建筑元素中,既美观又实用。
除了在建筑领域的应用外,圆柱和圆锥还在其他领域发挥着重要作用。在制造业中,圆柱形的零件和部件因其易于加工和制造的特性而广受欢迎。而圆锥形的零件则常被用于需要逐渐改变直径或角度的场合,如锥形齿轮、锥形轴承等。此外,在航空航天、机械工程、电子工程等领域中,圆柱和圆锥也扮演着举足轻重的角色。
在数学领域,圆柱和圆锥的关系更是得到了深入的研究。一方面,它们都是解析几何和立体几何中的重要研究对象,具有丰富的几何性质和定理。另一方面,它们也是微积分和向量分析等高等数学课程中的重要内容,为解决实际问题提供了有力的数学工具。
例如,在求解圆柱和圆锥的体积和表面积时,我们需要运用积分和极限等数学方法。这些方法的运用不仅加深了我们对圆柱和圆锥性质的理解,也为我们解决实际问题提供了更为精确和高效的手段。
此外,圆柱和圆锥在几何变换中也占据着重要地位。通过平移、旋转、缩放等几何变换,我们可以得到形状各异但本质相同的圆柱和圆锥。这些变换不仅丰富了我们对几何图形的认识,也为我们解决实际问题提供了更多的可能性和灵活性。
值得注意的是,圆柱和圆锥的关系还体现在它们的截面上。当用一个平面去截一个圆柱时,我们可以得到一个矩形、圆形、椭圆形或抛物线形的截面。同样地,当用一个平面去截一个圆锥时,我们也可以得到一个三角形、圆形、椭圆形或双曲线形的截面。这些截面的形状和性质不仅与截面的位置和方向有关,还与圆柱和圆锥本身的形状和尺寸有关。因此,通过研究截面形状和性质的变化规律,我们可以进一步揭示圆柱和圆锥之间的内在联系和本质特征。
在实际应用中,圆柱和圆锥的截面性质也具有重要意义。例如,在机械加工中,我们需要根据零件的形状和尺寸要求来选择合适的切削工具和切削方式。这时,了解圆柱和圆锥的截面性质就显得尤为重要。通过精确计算和分析截面形状和尺寸的变化规律,我们可以优化切削工艺和切削参数,提高加工效率和加工质量。
综上所述,圆柱和圆锥作为几何学中两种重要的立体图形,它们之间既存在着微妙的内在联系,又各自具有独特的形状和性质。这种关系不仅在数学理论中占据重要地位,更在实际应用中展现出无穷的魅力和实用性。因此,我们应该深入学习和理解圆柱和圆锥的性质及其相互关系,以便更好地应用它们来解决实际问题。
在未来的学习和工作中,我们还将继续探索圆柱和圆锥的更多性质和应用场景。随着科学技术的不断发展和进步,相信圆柱和圆锥将在更多领域发挥出更大的作用和价值。同时,我们也期待在未来的学习和研究中能够发现更多关于圆柱和圆锥的新性质和新应用,为人类的进步和发展做出更大的贡献。
- 上一篇: 如何轻松充值QQ里的Q币
- 下一篇: 如何取消淘宝的免密支付功能
-
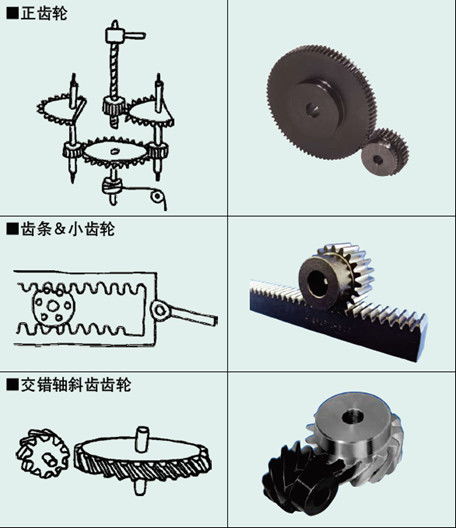 锥齿轮定义及与斜齿轮的主要区别资讯攻略11-17
锥齿轮定义及与斜齿轮的主要区别资讯攻略11-17 -
 如何使用雨量器计算降雨量资讯攻略11-10
如何使用雨量器计算降雨量资讯攻略11-10 -
 打造完美圆柱:一步步教你制作圆柱的详细方法资讯攻略11-23
打造完美圆柱:一步步教你制作圆柱的详细方法资讯攻略11-23 -
 自制圆柱形枕头指南资讯攻略02-09
自制圆柱形枕头指南资讯攻略02-09 -
 如何制作圆锥体的详细步骤资讯攻略11-14
如何制作圆锥体的详细步骤资讯攻略11-14 -
 揭秘!圆柱侧面积的神奇等式,你不可不知的几何奥秘资讯攻略10-26
揭秘!圆柱侧面积的神奇等式,你不可不知的几何奥秘资讯攻略10-26












