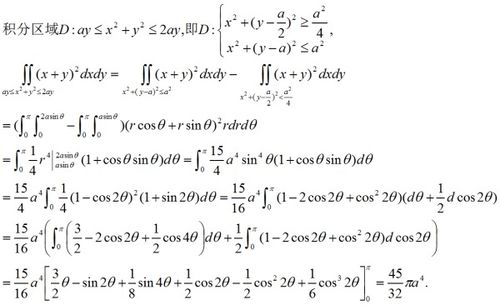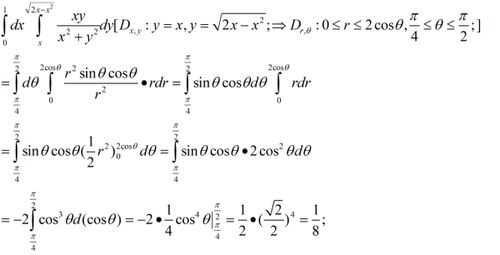二重积分计算方法揭秘,附上一个简单易懂例题解析
在数学的广阔天地里,二重积分如同一座桥梁,连接着对二维区域面积与体积的深刻理解和计算。它不仅是微积分的重要组成部分,更是解决物理、工程等领域诸多问题的得力工具。今天,我们就来一起揭开二重积分的神秘面纱,看看它是如何计算的,并通过一个简单的例题来加深理解。
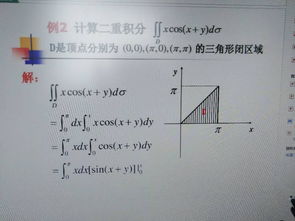
二重积分的基本概念
二重积分,简单来说,就是对一个二维平面区域上的函数进行积分。它可以看作是先对某一方向(比如x方向)进行一次积分(即定积分),然后再对另一个方向(比如y方向)进行积分。这个过程可以理解为“先积再积”,因此得名二重积分。
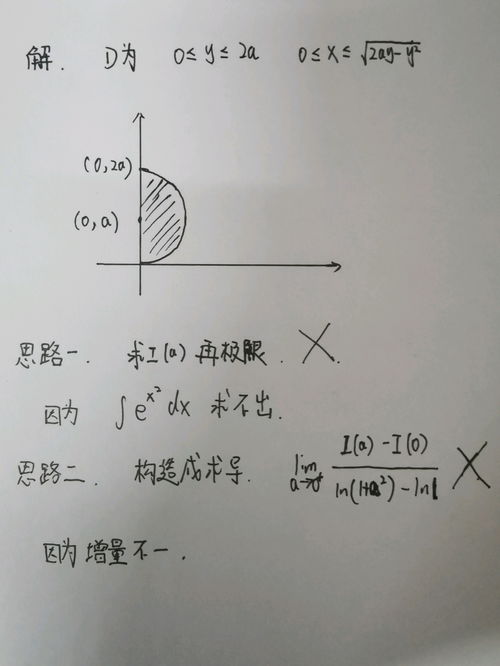
数学上,二重积分的表达式通常写作:

∫∫_D f(x, y) dxdy

其中,D表示被积分的区域,f(x, y)是被积函数,dxdy表示积分元素,即微小的面积。
二重积分的计算方法
二重积分的计算方法主要有两种:直角坐标系下的计算和极坐标系下的计算。这里,我们先介绍直角坐标系下的计算方法。
1. 确定积分区域:首先,要明确被积分的区域D。这个区域可以是矩形、圆形、三角形等各种形状。
2. 选择积分顺序:根据区域的特征和问题的便利性,选择先对x积分还是对y积分。这通常取决于区域的边界是否更容易用x或y的表达式来描述。
3. 写出积分表达式:根据选择的积分顺序,将区域D的边界表示为x或y的函数,并代入被积函数f(x, y)中,形成积分表达式。
4. 计算积分:按照定积分的计算方法,依次计算内层和外层的积分。
简单的例题解析
为了更直观地理解二重积分的计算过程,我们来看一个简单的例题。
例题:计算由直线y = x,曲线y = x^2,以及x轴所围成的平面图形D的面积S,并求该图形绕x轴旋转一周所形成的旋转体的体积V。
步骤一:确定积分区域
首先,我们绘制出直线y = x,曲线y = x^2,以及x轴的图像。通过观察,我们可以发现这三条曲线交于点(0,0)和(1,1),形成一个封闭的图形D。
步骤二:写出面积S的积分表达式
由于图形D在x方向上的范围是0到1,在y方向上的范围由y = x^2和y = x决定,我们可以选择先对y积分,再对x积分。因此,面积S的积分表达式为:
S = ∫_0^1 dx ∫_x^2^ ^x f(x, y) dy
其中,f(x, y)在这里可以看作是1(因为我们求的是面积,所以被积函数为1)。
将f(x, y)代入,得到:
S = ∫_0^1 dx ∫_x^2^ ^x 1 dy = ∫_0^1 (x - x^2) dx
步骤三:计算面积S
对上面的积分进行计算,得到:
S = [1/2*x^2 - 1/3*x^3]_0^1 = 1/2 - 1/3 = 1/6
所以,图形D的面积为1/6。
步骤四:写出体积V的积分表达式
接下来,我们求图形D绕x轴旋转一周所形成的旋转体的体积V。根据旋转体的体积公式,我们有:
V = π ∫_0^1 [(x)^2 - (x^2)^2] dx
这里,(x)^2表示直线y = x旋转后形成的圆的半径的平方,(x^2)^2表示曲线y = x^2旋转后形成的圆的半径的平方。
步骤五:计算体积V
对上面的积分进行计算,得到:
V = π ∫_0^1 (x^2 - x^4) dx = π [1/3*x^3 - 1/5*x^5]_0^1 = π*(1/3 - 1/5) = 2π/15
所以,图形D绕x轴旋转一周所形成的旋转体的体积为2π/15。
总结
通过上面的例题,我们可以看到二重积分在求解二维平面图形的面积和旋转体的体积时的重要作用。在实际应用中,二重积分还可以用于求解平面图形的质量、重心、转动惯量等物理量,以及求解热传导、静电场等物理问题中的面积分和体积分。
在计算二重积分时,关键是要确定好积分区域和积分顺序,并正确地写出积分表达式。然后,按照定积分的计算方法,依次计算内层和外层的积分。虽然过程可能有些复杂,但只要我们掌握了基本的方法和技巧,就能够轻松地解决各种问题。
希望这篇文章能够帮助你更好地理解二重积分的计算方法和应用。在未来的学习和工作中,当你遇到与二重积分相关的问题时,不妨回顾一下这篇文章,相信你会有更多的收获和启发。
- 上一篇: 如何使用百度地图定位当前位置
- 下一篇: 帝国时代2全秘籍指南,轻松称霸战场!
-
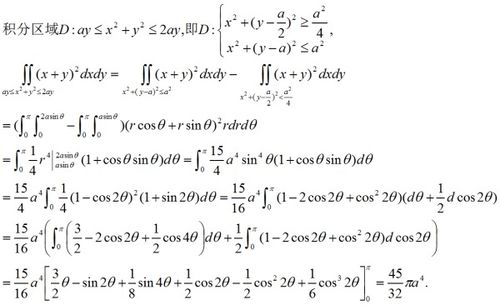 掌握二重积分dxdy的计算方法,轻松解题无烦恼资讯攻略10-24
掌握二重积分dxdy的计算方法,轻松解题无烦恼资讯攻略10-24 -
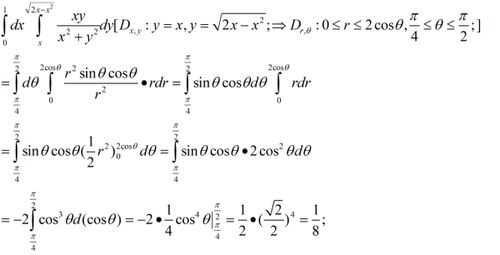 全面掌握!24个必备二重积分公式精选集资讯攻略01-18
全面掌握!24个必备二重积分公式精选集资讯攻略01-18 -
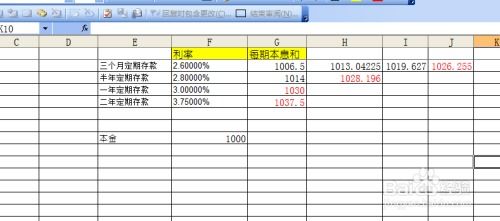 揭秘:银行利率的计算奥秘资讯攻略11-18
揭秘:银行利率的计算奥秘资讯攻略11-18 -
 揭秘!入学积分查询全攻略,一网打尽!资讯攻略11-30
揭秘!入学积分查询全攻略,一网打尽!资讯攻略11-30 -
 揭秘:二重感染究竟是什么?资讯攻略11-24
揭秘:二重感染究竟是什么?资讯攻略11-24 -
 曲线积分的计算方法资讯攻略10-31
曲线积分的计算方法资讯攻略10-31